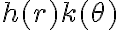Buenas,
Tengo una duda con respecto a este ejercicio y porque no es 0 el limite. Si yo paso a polares, los terminos de la funcion me quedan todos multiplicados por r, y entonces el limite con r-->0 seria 0, pero dice que probar que NO existe.
Preciso ayuda para terminar de entender.
Muchas gracias.
del numerador y del denominador se te van a cancelar, por lo tanto te va a terminar quedando una expresión que depende sólo de 
. Revisá las cuentas porque probablemente se te haya escapado algún detalle. y que va a 
, producto con algo que depende sólo de . Necesitamos también que lo que dependa de sea acotado. Lo aclaro por las dudas para algún otro límite donde llegue a pasar eso.
con 
sólo dependiendo de y 
sólo dependiendo de . Lo que comentaba era que el ejercicio 4e nos dice que si tiende a cuando tiende a 0 y está acotada, entonces el límite de 
es . Si la función no es acotada no podemos utilizar esta propiedad, un ejemplo es el ejercicio 5c. No estamos hablando allí de que el límite dependa de , el límite direccional siempre da en ese caso.