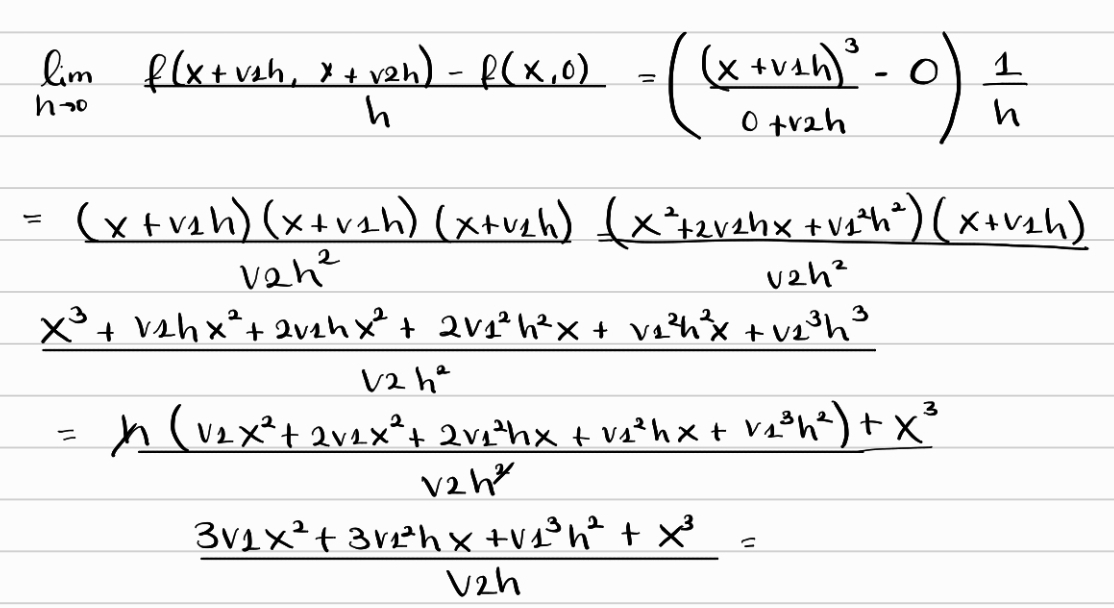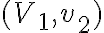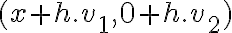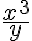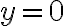Hola, en este ejercicio estudie las derivadas direccionales para (x,0) y me queda este limite. Llegue a que cuando x=0, el limite da 0 por lo tanto existe la derivada direccional pero no se como generalizarlo para cualquier x.
Hola Ayelén,
Ahí lo estás haciendo para 
genérico, es decir, para cualquier punto del plano que sea de la forma 
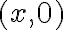. La sustitución que hacés es para el caso 
, sino al evaluar 
en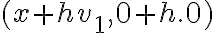 
la función tiene otra fórmula, por lo que las direcciones de la forma 
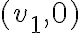tendrías que estudiarlas aparte. Para el caso en el que lo hacés, cuando calculás el límite, sin llegar a desarrollar, el límite del numerador es y el del denominador es 
, por lo que si es distinto de ese límite no existe, y si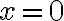 
entonces es una indeterminación e intentamos resolverla. Luego por otra parte quedarían ver las derivadas direccionales en los puntos 
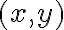con 
.
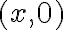genérico, es decir, para cualquier punto del plano que sea de la forma . La sustitución que hacés es para el caso , sino al evaluar en 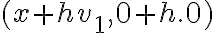la función tiene otra fórmula, por lo que las direcciones de la forma 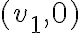tendrías que estudiarlas aparte. Para el caso en el que lo hacés, cuando calculás el límite, sin llegar a desarrollar, el límite del numerador es y el del denominador es , por lo que si es distinto de ese límite no existe, y si 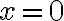entonces es una indeterminación e intentamos resolverla. Luego por otra parte quedarían ver las derivadas direccionales en los puntos 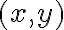con .Agrego como comentario que en todas esas igualdades habría que escribir el límite, no solamente las expresiones algebraicas.
Saludos,
Leandro
Buenas, quería saber si estaría bien este procedimiento para confirmar que la derivada direccional no existe en cierto punto, hago el limite y me queda un h en el denominador entonces el limite se me iría a infinito. Pero cuando el limite me da un numero fijo si puedo afirmar que existe.
El razonamiento que comentás es correcto si el límite del numerador no es , sino tendrías una indeterminación y habría que resolverla. Cuando el límite te da un valor real ahí sí existe la derivada direccional y ese es su valor.
Saludos,
Leandro
, sino tendrías una indeterminación y habría que resolverla. Cuando el límite te da un valor real ahí sí existe la derivada direccional y ese es su valor.Saludos,
Leandro
Hola, me surgió una duda del planteo hecho, porque si tomamos (v1,v2) genéricos para el punto(x,0) nos da que el limite tiende a infinito por lo tanto las derivadas direccionales no existen pero cuando resolvemos el limite en la dirección (v1,0) la derivada direccional si existe. El primer limite no nos sirve para afirmar que la derivada no va a existir en cualquier dirección (v1,v2)?Gracias
Hola Ayelén,
No lo estás haciendo para
genéricos sino para aquellos con . Cuando evaluás en 
estás usando la fórmula 
, por lo tanto, estás asumiendo que no pertenece a la recta 
, y eso pasa si y sólo si .
Saludos,
Leandro
No lo estás haciendo para
genéricos sino para aquellos con . Cuando evaluás en estás usando la fórmula , por lo tanto, estás asumiendo que no pertenece a la recta , y eso pasa si y sólo si .Saludos,
Leandro