Foro de Práctico

Hola,

Estoy con dudas al intentar demostrar esto. Mi idea es utilizar el hecho de que una relación de equivalencia queda determinada por una partición del conjunto sobre el cual estará definida la relación; así, el conjunto de estas particiones será el conjunto cociente. Bueno, la pregunta es, entonces, ¿De cuántas maneras se puede particionar un conjunto con 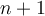$n+1$ elementos, de tal forma que los subconjuntos sean disjuntos dos a dos? 

Para responder esto, se me ocurrió separar en casos y aplicar la regla de la suma, pero no estoy seguro de que esté bien. Primero voy a comentar lo primero que se me ocurrió, lo cual me lleva a un resultado incorrecto:

Caso genérico 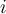$i$:  Considero 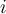$i$ elementos del conjunto, los cuales se pueden elegir de $\binom{n+1}{i}$ formas distintas. Formo una relación de equivalencia con los $n+1-i$ elementos restantes, lo cual se puede hacer de $R_{n+1-i}$ formas. 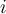Esto último me da una partición del subconjunto de $n+1-i$ elementos, para completar la partición que determina la relación sobre el conjunto total, le agrego la clase de equivalencia que consta de los $i$ elementos elegidos al principio. Así, este caso se puede realizar de $\binom{n+1}{i} R_{n+1-i}$ formas.

Por la regla de la suma, y considerando $1 \leq i \leq n+1$, se tiene $R_{n+1} = \binom{n+1}{1}R_n + \binom{n+1}{2}R_{n-1} + \dots + \binom{n+1}{n+1}R_0$. Imagino que estoy contando casos de más, esto me forzó a pensar en lo siguiente:

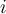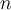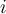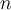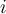Caso genérico $i$: entre los primeros $n$ elementos del conjunto, elijo $i$, lo cual se puede hacer de $\binom{n}{i}$ formas. Con los restantes $n-i$ elementos (entre los primeros $n$ del conjunto total), formo una relación de equivalencia, lo cual se puede realizar de $R_{n-i}$ formas. Ahora bien, para completar la partición, agrego la relación de equivalencia que consta de los $i$ elementos elegidos previamente y el último, que hasta el momento no había sido considerado. Así, este caso se puede realizar de $\binom{n}{i} R_{n-i}$ formas.

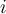En lo anterior se supuso $n-i \geq 0$, por lo que $i$ debe verificar 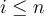$i \leq n$. Además, el mínimo valor posible para 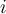$i$ es 0 (valores negativos no tienen sentido y con un valor mínimo mayor no se cubren todos los casos). Luego, por la regla de la suma, $R_{n+1} = \binom{n}{0}R_n + \binom{n}{1}R_{n-1} + \dots + \binom{n}{n}R_{0}$.

¿Está bien esto último? ¿Estoy contando de más en el primer razonamiento? ¿Por qué? Gracias!

Saludos,

Leandro