Hola, en estos ejercicios no me queda claro como tomarme el máximo entre las dos funciones. Tendría que ir evaluando en distintos k? Porque para k= 0 x=0 e y= 0 pero luego para un k menor a 0, x sería vacío? pero en y si habría conjuntos de nivel?Gracias
Buenas,
Es de utilidad primero estudiar en qué región del plano es mayor cada una de las dos funciones. Por ejemplo si queremos estudiar la función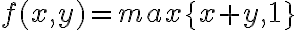 , queremos ver cuándo
, queremos ver cuándo 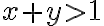 y cuándo
y cuándo 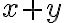 . Esto lo resolvemos viendo dónde sucede la igualdad, que en este caso es la recta
. Esto lo resolvemos viendo dónde sucede la igualdad, que en este caso es la recta 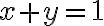 , y luego tenemos dos semiplanos donde en uno que llamaremos
, y luego tenemos dos semiplanos donde en uno que llamaremos 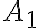 la función vale
la función vale 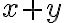 y en el otro que llamaremos
y en el otro que llamaremos 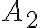 la función vale
la función vale  .
.
Una vez tenemos esto, si queremos encontrar el conjunto de nivel correspondiente al valor , lo que hacemos es ver cuándo
, lo que hacemos es ver cuándo 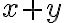 vale
vale  y nos quedamos solamente con aquellos puntos que están en
y nos quedamos solamente con aquellos puntos que están en 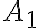 , y por otro lado vemos cuándo la función
, y por otro lado vemos cuándo la función  vale
vale  y lo cortamos con el semiplano
y lo cortamos con el semiplano 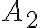 . En definitiva lo que tenemos es una función partida, por lo que tenemos que utilizar en cada región una fórmula distinta.
. En definitiva lo que tenemos es una función partida, por lo que tenemos que utilizar en cada región una fórmula distinta.
Como detalle final, en el lugar donde se da la igualdad va a ser lo mismo calcular con cualquiera de las dos funciones cuáles son los puntos tal que su imagen es .
.
Saludos,
Leandro
Es de utilidad primero estudiar en qué región del plano es mayor cada una de las dos funciones. Por ejemplo si queremos estudiar la función
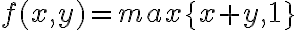 , queremos ver cuándo
, queremos ver cuándo 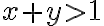 y cuándo
y cuándo 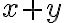 . Esto lo resolvemos viendo dónde sucede la igualdad, que en este caso es la recta
. Esto lo resolvemos viendo dónde sucede la igualdad, que en este caso es la recta 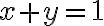 , y luego tenemos dos semiplanos donde en uno que llamaremos
, y luego tenemos dos semiplanos donde en uno que llamaremos 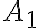 la función vale
la función vale 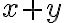 y en el otro que llamaremos
y en el otro que llamaremos 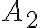 la función vale
la función vale  .
.Una vez tenemos esto, si queremos encontrar el conjunto de nivel correspondiente al valor
 , lo que hacemos es ver cuándo
, lo que hacemos es ver cuándo 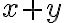 vale
vale  y nos quedamos solamente con aquellos puntos que están en
y nos quedamos solamente con aquellos puntos que están en 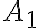 , y por otro lado vemos cuándo la función
, y por otro lado vemos cuándo la función  vale
vale  y lo cortamos con el semiplano
y lo cortamos con el semiplano 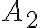 . En definitiva lo que tenemos es una función partida, por lo que tenemos que utilizar en cada región una fórmula distinta.
. En definitiva lo que tenemos es una función partida, por lo que tenemos que utilizar en cada región una fórmula distinta.Como detalle final, en el lugar donde se da la igualdad va a ser lo mismo calcular con cualquiera de las dos funciones cuáles son los puntos tal que su imagen es
 .
.Saludos,
Leandro
