Buenas, no sé cómo seguir con este ejercicio:

Llegué sí a que  pero no sé cómo hallar ese
pero no sé cómo hallar ese  que me piden.
que me piden.

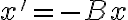 es
es 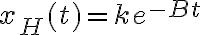 . Luego encontraste una solución particular a la ecuación
. Luego encontraste una solución particular a la ecuación 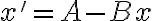 que es
que es  . El siguiente paso es sumarlas, es decir, tenemos que la solución general a la ecuación
. El siguiente paso es sumarlas, es decir, tenemos que la solución general a la ecuación 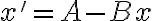 es
es 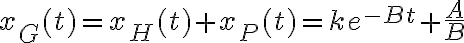 .
. , y luego buscar lo que nos pide resolver el ejercicio. Fijate si podés terminarlo con esas cosas y sino cualquier cosa volvés a escribir por acá.
, y luego buscar lo que nos pide resolver el ejercicio. Fijate si podés terminarlo con esas cosas y sino cualquier cosa volvés a escribir por acá.