Hola, Lorena:
En efecto, haces bien arrancando con Euler para tener que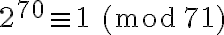 . Recuerda que llegados a este punto, la idea es dividir el exponente original del problema, en este caso
. Recuerda que llegados a este punto, la idea es dividir el exponente original del problema, en este caso 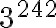 entre 70 para poder encontrar el resto de dividir
entre 70 para poder encontrar el resto de dividir 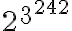 entre 71. En otras palabras, la idea es hallar
entre 71. En otras palabras, la idea es hallar  entre 0 y 69 tal que
entre 0 y 69 tal que 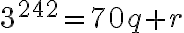 , ya que a partir de allí puedes elevar a la
, ya que a partir de allí puedes elevar a la  la congruencia
la congruencia 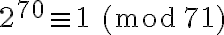 y después multiplicar la congruencia resultante por
y después multiplicar la congruencia resultante por 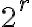 (fíjate que no importa cuánto vale
(fíjate que no importa cuánto vale  ). Entonces, lo que importa hallar es tal
). Entonces, lo que importa hallar es tal  , es decir, resolver
, es decir, resolver 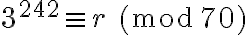 .
.
Espero que lo anterior sea de utilidad.
Saludos,
Marco
En efecto, haces bien arrancando con Euler para tener que
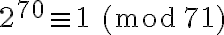 . Recuerda que llegados a este punto, la idea es dividir el exponente original del problema, en este caso
. Recuerda que llegados a este punto, la idea es dividir el exponente original del problema, en este caso 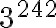 entre 70 para poder encontrar el resto de dividir
entre 70 para poder encontrar el resto de dividir 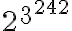 entre 71. En otras palabras, la idea es hallar
entre 71. En otras palabras, la idea es hallar  entre 0 y 69 tal que
entre 0 y 69 tal que 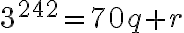 , ya que a partir de allí puedes elevar a la
, ya que a partir de allí puedes elevar a la  la congruencia
la congruencia 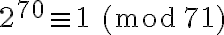 y después multiplicar la congruencia resultante por
y después multiplicar la congruencia resultante por 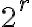 (fíjate que no importa cuánto vale
(fíjate que no importa cuánto vale  ). Entonces, lo que importa hallar es tal
). Entonces, lo que importa hallar es tal  , es decir, resolver
, es decir, resolver 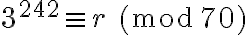 .
. Espero que lo anterior sea de utilidad.
Saludos,
Marco
