Parciales y exámenes

Buenas,

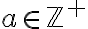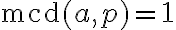En la consulta de las 16:00 habíamos probado que, dados $a\in\mathbb{Z}^+$ y $p$ primo con ${\rm mcd}(a,p) = 1$, para cada 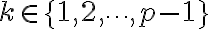$k \in \{ 1, 2, \dots, p-1 \}$ existe un único 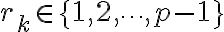$r_k \in \{ 1, 2, \dots, p-1 \}$ tal que 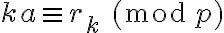$ka \equiv r_k \ ({\rm mod} \ p)$. Quedó pendiente probar a partir de esto que $a^{p-1} \equiv 1 \ ({\rm mod} \ p$. 

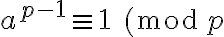Tenemos la siguiente lista de congruencias: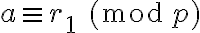

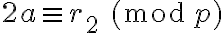
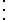
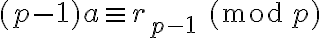
$a \equiv r_1 \ ({\rm mod} \ p)$
$2a \equiv r_2 \ ({\rm mod} \ p)$
$\vdots$
$(p-1)a \equiv r_{p-1} \ ({\rm mod} \ p)$

Podemos multiplicar todas esas congruencias y obtener: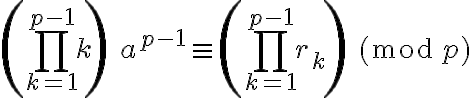

$\left( \prod^{p-1}_{k = 1} k \right) \ a^{p-1} \equiv \left( \prod^{p-1}_{k = 1} r_k \right) \ ({\rm mod} \ p)$.

Note que 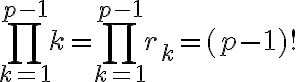$\prod^{p-1}_{k = 1} k = \prod^{p-1}_{k = 1} r_k = (p-1)!$

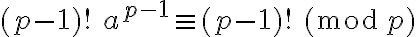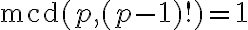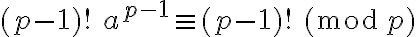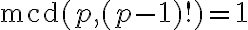Entonces, $(p-1)! \ a^{p-1} \equiv (p-1)! \ ({\rm mod} \ p)$. Luego, como $p$ es primo, se tiene que ${\rm mcd}(p, (p-1)!) = 1$. Por el lema de Euclides, se tiene que $(p-1)! \ a^{p-1} \equiv (p-1)! \ ({\rm mod} \ p)$ y ${\rm mcd}(p, (p-1)!) = 1$ implica que 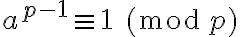$a^{p-1} \equiv 1 \ ({\rm mod} \ p)$. Queda demostrado.

Saludos cordiales,
Marco