Buenas tardes,
Hoy en la consulta se estuvo trabajando el problema de probar que 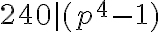 . Intentamos usar el hecho de que
. Intentamos usar el hecho de que  es de la forma
es de la forma 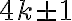 seguido de un argumento de inducción, pero no resultó. Las ideas que vimos sirven para resolver esto, pero antes debe simplificarse el problema.
seguido de un argumento de inducción, pero no resultó. Las ideas que vimos sirven para resolver esto, pero antes debe simplificarse el problema.
Primero notemos que lo que se pide demostrar es equivalente a probar que la congruencia 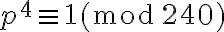 se cumple. Por otro lado, como
se cumple. Por otro lado, como 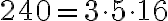 y además
y además 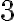 ,
, 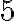 y
y 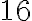 son coprimos dos a dos, demostrar la congruencia
son coprimos dos a dos, demostrar la congruencia 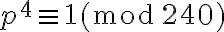 es equivalente a demostrar que se cumplen las siguientes tres congruencias de forma simultánea:
es equivalente a demostrar que se cumplen las siguientes tres congruencias de forma simultánea:
(I) 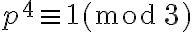 ,
,
(II) 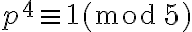 , y
, y
(III) 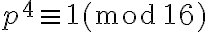 .
.
Como  es cualquier primo mayor o igual que 7, tenemos que
es cualquier primo mayor o igual que 7, tenemos que  es coprimo con 3, 5 y 16. Por el Teorema de Fermat-Euler, tenemos que
es coprimo con 3, 5 y 16. Por el Teorema de Fermat-Euler, tenemos que 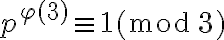 y
y 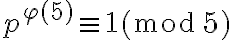 , donde
, donde 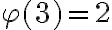 y
y 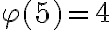 , ya que 3 y 5 son primos. Entonces,
, ya que 3 y 5 son primos. Entonces, 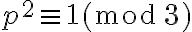 , y si elevamos al cuadrado esta congruencia se obtiene
, y si elevamos al cuadrado esta congruencia se obtiene 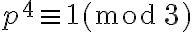 , es decir, se cumple (I). Por otro lado, de
, es decir, se cumple (I). Por otro lado, de 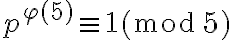 se tiene directamente que
se tiene directamente que 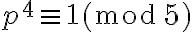 , es decir, se cumple (II).
, es decir, se cumple (II).
La congruencia (III) es la más delicada de demostrar. Para empezar, no nos sirve el Teorema de Fermat-Euler pues 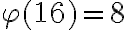 , de donde se tendría
, de donde se tendría 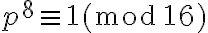 , pero lo que necesitamos es
, pero lo que necesitamos es 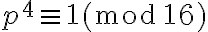 . Llegados a este punto, una manera de resolver la congruencia es usando el dato de que
. Llegados a este punto, una manera de resolver la congruencia es usando el dato de que 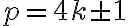 para algún
para algún 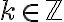 . En efecto, vemos que:
. En efecto, vemos que: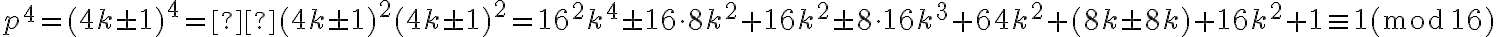 .
.
Por lo tanto, la congruencia (III) también se satisface.
Saludos cordiales,
Marco
240 divide a p^4 - 1, donde p es cualquier primo mayor o igual que 7
de Marco Antonio Perez -
Número de respuestas: 0
