Buenas, no sé cómo empezar con este ejercicio

para  tendría que verificar si A es abierto o no, sé que A es abierto sii
tendría que verificar si A es abierto o no, sé que A es abierto sii  donde
donde  es el conjunto de puntos interiores, pero no sé cómo aplicar la definición en este caso
es el conjunto de puntos interiores, pero no sé cómo aplicar la definición en este caso
 . Para estudiar si un conjunto es abierto tenemos que ver si todos sus puntos son interiores. En este caso nuestro conjunto está formado por dos cuartos del círculo unidad. Hay que ver para todos los puntos tenemos algún entorno sólo compuesto por puntos de
. Para estudiar si un conjunto es abierto tenemos que ver si todos sus puntos son interiores. En este caso nuestro conjunto está formado por dos cuartos del círculo unidad. Hay que ver para todos los puntos tenemos algún entorno sólo compuesto por puntos de  o si hay algún punto
o si hay algún punto  que no importa que tan pequeño nos tomemos un
que no importa que tan pequeño nos tomemos un 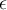 siempre vamos a tener algún punto en
siempre vamos a tener algún punto en  que no pertenezca a
que no pertenezca a  . Para esto te recomiendo mirar los "bordes" del conjunto (en el sentido coloquial de la palabra). Avisame si con eso te sale y sino volveme a comentar nomás.
. Para esto te recomiendo mirar los "bordes" del conjunto (en el sentido coloquial de la palabra). Avisame si con eso te sale y sino volveme a comentar nomás. te delimita el conjunto entre dos rectas, que las incluye porque la desigualdad no es estricta. La condición que está contenida en el círculo es
te delimita el conjunto entre dos rectas, que las incluye porque la desigualdad no es estricta. La condición que está contenida en el círculo es 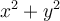 , y no incluye la circunsferencia (el borde del círculo) porque la desigualdad es estricta. No es una bola la que tiene que tener puntos de fuera del conjunto, es que toda bola tenga puntos de fuera del conjunto, que es lo que va a suceder efectivamente con los pts que estén en
, y no incluye la circunsferencia (el borde del círculo) porque la desigualdad es estricta. No es una bola la que tiene que tener puntos de fuera del conjunto, es que toda bola tenga puntos de fuera del conjunto, que es lo que va a suceder efectivamente con los pts que estén en  y sean parte de esas dos rectas.
y sean parte de esas dos rectas. es la unión de
es la unión de  y
y 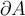 . Así que la afirmación va a ser cierta si
. Así que la afirmación va a ser cierta si  contiene todos sus puntos frontera.
contiene todos sus puntos frontera.