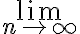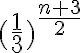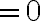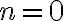Foro Práctico 4

Buenas, el ejercicio 1b consiste en identificar si la siguiente serie es convergente, y si lo es, calcular su suma:

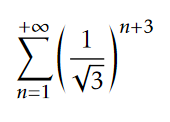
Lo primero que hice fue fijarme el criterio necesario (que el término general de la serie tenga limite igual a cero cuando n tiende a infinito). Para ello, me fije que:

$\lim_{n\to\infty}$  ${(\frac{1}{3}})^{\frac{n+3}{2}}$ $= 0$

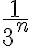
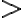
Para clasificarlo, me fije que, por el criterio de comparación y por el ejercicio anterior: 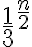$\frac{1}{3^{n}}$ $>$ ${\frac{1}{3}}^{\frac{n}{2}}$, y como la primera converge, ello implica que está acotada, por lo tanto por la desigualdad la segunda también está acotada, y además las sucesiones enésimas son monótonas crecientes, por tanto, la segunda también converge.

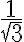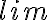
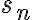
Hasta ahí, creo que esta todo bien. El tema viene ahora, y es que para calcular el límite de la sucesión enésima me fije que es una serie geométrica de término general $\frac{1}{\sqrt{3}}$, y como el término general es menor en valor absoluto que 1, puedo usar la siguiente igualdad (extraída de las notas del curso, pp37, ej2.35): 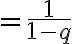$lim$ $s_{n}$ $= \frac{1}{1-q}$ siendo q el término general. 

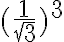
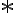
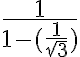
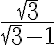
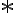
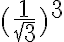
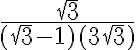
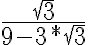
Entonces, el desarrollo me queda: $(\frac{1}{\sqrt{3}})^{3}$ $*$ $\frac{1}{1 - (\frac{1}{\sqrt{3}})}$ $=$ $\frac{\sqrt{3}}{\sqrt{3} - 1}$ $*$ $(\frac{1}{\sqrt{3}})^{3}$ $=$ $\frac{\sqrt{3}}{(\sqrt{3} - 1)(3\sqrt{3})}$ $=$ $\frac{\sqrt{3}}{9 - 3*\sqrt{3}}$

Este resultado vendría a ser el resultado del limite de la sucesión enésima, por tanto, la suma infinita de la serie. Pero fijándome las soluciones, no es el caso. Vi que en los teóricos presenciales vieron otra forma de definir el limite de una serie geométrica, pero en las notas esa forma no esta. No entendí muy bien cual es el error porque, hasta donde llego a ver, los cálculos están bien hechos y las hipótesis necesarias para realizarlos se cumplen todas. Agradezco cualquier comentario, muchas gracias.