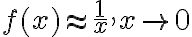Foro Práctico 5

Buenas noches, tengo una duda respecto a este problema:

Vi que 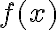$f(x)$ tiene problemas en 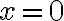$x=0$ así que traté de buscarle un equivalente, haciendo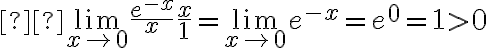 $\lim_{x\to 0} \frac{e^{-x}}{x}\frac{x}{1}= \lim_{x\to 0} e^{-x}=e^0=1>0$

$f(x)\approx \frac{1}{x}, x\rightarrow 0$

Luego, 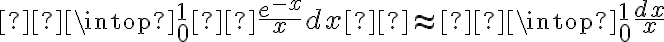$\intop\nolimits_{0}^{1}  \frac{e^{-x}}{x}dx  \approx  \intop\nolimits_{0}^{1}\frac{dx}{x}$ y como la segunda integral diverge (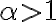$\alpha > 1$), su equivalente es de la misma clase (la integral original también diverge)

No sé si está bien razonado de esa forma. 

También tengo la duda de por qué 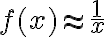$f(x) \approx \frac{1}{x}$, ¿es por lo que mencioné al principio o hay alguna otra razón?