tengo problemas para parametrizar la curva de la parte b)
no llego a nadaa! graciasss
Hola,
tenés que despejar la ecuación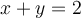 
en la otra; de ahí te queda una ecuación en x (o y dependiendo de cuál despejaste) y en z. Despejas z y te va a quedar que es igual a más,menos una raíz. La curva que necesitas es la unión de ambas curvas, en el sentido que se pide. Usando la propiedad que dice que la integral sobre una curva es igual a la suma de las integrales sobre las curvas que son unión de la primera, llegas al resultado.
Espero ahber sido claro,
Saludos
Hola!, Yo plante todo bastante similar y llegue a que el resultado es:
2*raiz(2)*pi, se ve que algo tengo mal.
¿Vos llegaste a la solución?
La parametrizacion te quedo:
x= 2-t
y= t
z= (+/-) (4t-2t^2)^(1/2)
0 <= t <= 2
Agradezco cualquier ayuda :D
Haciendo como vos hiciste Martín, llegué a lo mismo en z, y como no me daba cuenta como parametrizar, hice y=t y cambié en todos lados por t según corresponda (eso es lo que hiciste vos no?), integrando eso me quedaron 0 ambas integrales.
Yo no entiendo bien como llegar a los puntos iniciales y finales de la curva. Tengo el ejercicio que copie del practico y no me queda clara esa parte, como despeja.
Saludos
yo llegue a la misma parametrización que vos, pero no me doy cuenta porque es de 0 a 2 la integral. No entiendo bien como sacar los limites de integración, porque te dice solo el sentido y nada mas.
si sustituis la primera ecuación en la segunda te queda la ecuación de una esfera de centro (0,0,0) y radio 2, pero no se como parametrizar una esfera, me supongo que debe haber una forma sencilla
En respuesta a Joaquin Camilo Podesta Ceschi
Re: practico 3 - ej 3
Hola, yo tengo problemas con la parte b) y c), no me doy cuenta de los limites de integracion. Alguien me puede ayudar? Gracias
Hice lo mismo que uds y también tengo problemas con los limites de integración.
Pero me surgió una duda: si sustituis x+y=2 en la otra ecuación va a quedarte la ecuación de una esfera, la cual se podría parametrizar por esféricas.
Si lo hago de esa forma tengo problemas porque me quedan dos parámetros y no se como calcular el producto escalar para luego integrar.
Intente hacerlo por coordenadas esfericas y me tope con tu mismo problema patricia.
Despues lo que hice fue obtener la ecuación de la esfera de radio 2 (x^2 + y^2 +z^2 = 4), para luego decir que como y = 2 -x, entonces y^2 = x^2 -4x +4.
Paso siguiente pongo a y^2 en la ecuacion de la esfera y obtengo a z en funcion de x.
Luego hago el C.V x = t, entonces y = 2 -t, entonces z = masmenosALGO.
Una vez tenidos todos esos elementos, puedo saber la curva parametrizada p(t) y su derivada, y puedo hacer el producto escalar:
<(Y,Z,X),(derivada p(t))>
Una vez determinado ese producto escalar, y sustituido los Y,Z y X por sus valores con el parametro "t", puedo decir que tengo al "cuerpo" de la derivada, solo me faltan los intervalos.
Yo pense que como x = t, se movia entre -2 y 2, esos serían los intervalos a escojer, pero hago la cuenta en wolframalpha.com, y me da unos numeros complejos.
Yo pensaba hacer eso con el Z positivo, y luego con el Z negativo.
En el siguiente link podran ver a la integral que llegue. (Parte con z positivo)
http://www.wolframalpha.com/input/?i=integrate+%282+%2Bx+-sqrt%284x+-+2x%5E2%29++%2B%28sqrt%282%29*x*%281-x%29%29%2F%28%282x+-+x%5E2%29%5E%281%2F2%29%29%29+
La verdad que esta dificil esta parte... yo la dejo por ahi, sino no avanzo mas. Si algun/a groso/a sabe como ayudarnos, bienvenido sea.