Hola Ayelén,
Primero, con la desigualdad ya alcanza porque luego si la función que queremos integrar es convergente, como la integral de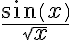 también es convergente, la resta nos quedaría de ambas nos quedaría convergente pero acabamos de ver que no lo es.
también es convergente, la resta nos quedaría de ambas nos quedaría convergente pero acabamos de ver que no lo es.
Para la integral de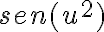 te recomiendo multiplicar y divider por
te recomiendo multiplicar y divider por 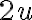 y ahí sí aplicar lo que dice el ejercicio 5.
y ahí sí aplicar lo que dice el ejercicio 5.
Por último, para estudiar la integral de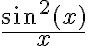 podemos usar la peridicidad del númerador y compararlo en cada intervalo de la forma
podemos usar la peridicidad del númerador y compararlo en cada intervalo de la forma ![[k\pi , (k+1) \pi] [k\pi , (k+1) \pi]](https://eva.fing.edu.uy/filter/tex/pix.php/aa8adb907d43075c1bd3fa35c3fa6a4f.gif) , y luego hacer la suma infinita. Es decir, tenemos que estudiar la integral en cada uno de esos intervalos y probar que es más grande que algo del orden de
, y luego hacer la suma infinita. Es decir, tenemos que estudiar la integral en cada uno de esos intervalos y probar que es más grande que algo del orden de 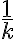 . Primero podemos ver que
. Primero podemos ver que 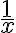 en ese intervalo es mayor a
en ese intervalo es mayor a 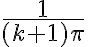 . Luego sabemos que
. Luego sabemos que 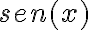 es mayor a
es mayor a 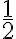 si nos restringimos al intervalo más pequeño
si nos restringimos al intervalo más pequeño ![[k\pi + \frac{1}{6} \pi, k\pi + \frac{5}{6} \pi ] [k\pi + \frac{1}{6} \pi, k\pi + \frac{5}{6} \pi ]](https://eva.fing.edu.uy/filter/tex/pix.php/a865e0058a29826d89846ed74b3effd8.gif) . Entonces conseguimos ver que
. Entonces conseguimos ver que
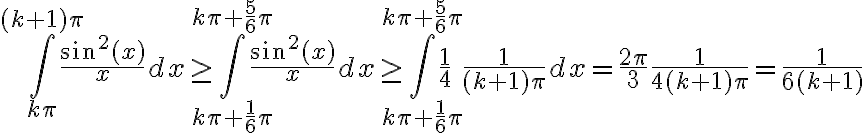
Luego sumando los infinitos términos obtenemos que la integral diverge.
Te sugiero hacer la representación gráfica de esta última parte, es decir, graficar un bosquejo de la función y del rectángulo que estamos construyendo dentro del área que queremos calcular, de forma de ayudar a seguir el hilo del razonamiento. Comentame nomás si no se entiende bien alguna parte de lo que puse o si te surge alguna duda.
Saludos,
Leandro
Primero, con la desigualdad ya alcanza porque luego si la función que queremos integrar es convergente, como la integral de
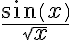 también es convergente, la resta nos quedaría de ambas nos quedaría convergente pero acabamos de ver que no lo es.
también es convergente, la resta nos quedaría de ambas nos quedaría convergente pero acabamos de ver que no lo es.Para la integral de
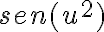 te recomiendo multiplicar y divider por
te recomiendo multiplicar y divider por 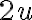 y ahí sí aplicar lo que dice el ejercicio 5.
y ahí sí aplicar lo que dice el ejercicio 5.Por último, para estudiar la integral de
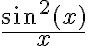 podemos usar la peridicidad del númerador y compararlo en cada intervalo de la forma
podemos usar la peridicidad del númerador y compararlo en cada intervalo de la forma ![[k\pi , (k+1) \pi] [k\pi , (k+1) \pi]](https://eva.fing.edu.uy/filter/tex/pix.php/aa8adb907d43075c1bd3fa35c3fa6a4f.gif) , y luego hacer la suma infinita. Es decir, tenemos que estudiar la integral en cada uno de esos intervalos y probar que es más grande que algo del orden de
, y luego hacer la suma infinita. Es decir, tenemos que estudiar la integral en cada uno de esos intervalos y probar que es más grande que algo del orden de 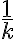 . Primero podemos ver que
. Primero podemos ver que 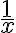 en ese intervalo es mayor a
en ese intervalo es mayor a 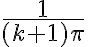 . Luego sabemos que
. Luego sabemos que 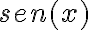 es mayor a
es mayor a 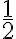 si nos restringimos al intervalo más pequeño
si nos restringimos al intervalo más pequeño ![[k\pi + \frac{1}{6} \pi, k\pi + \frac{5}{6} \pi ] [k\pi + \frac{1}{6} \pi, k\pi + \frac{5}{6} \pi ]](https://eva.fing.edu.uy/filter/tex/pix.php/a865e0058a29826d89846ed74b3effd8.gif) . Entonces conseguimos ver que
. Entonces conseguimos ver que 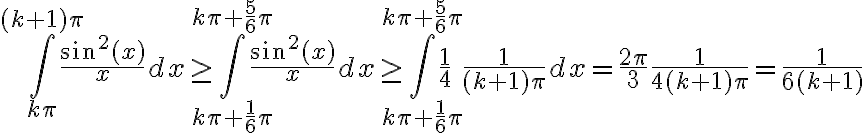
Luego sumando los infinitos términos obtenemos que la integral diverge.
Te sugiero hacer la representación gráfica de esta última parte, es decir, graficar un bosquejo de la función y del rectángulo que estamos construyendo dentro del área que queremos calcular, de forma de ayudar a seguir el hilo del razonamiento. Comentame nomás si no se entiende bien alguna parte de lo que puse o si te surge alguna duda.
Saludos,
Leandro
