Hola Alexis
Como el límite en infinito es L>0, existe un real K tal a partir del cual la función es más grande que L/2 (es decir, tomando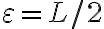 y aplicando la definición de límite).
y aplicando la definición de límite).
Entonces, si querés podés partir la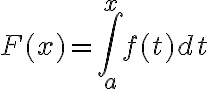 como la siguiente suma:
como la siguiente suma: 
La primera integral es un número, una constante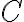 , y usando que
, y usando que  es más grande que
es más grande que 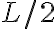 en la segunda integral, podés acotar
en la segunda integral, podés acotar 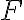 por algo como
por algo como  , y por lo tanto no puede tener límite finito cuando
, y por lo tanto no puede tener límite finito cuando  tiende a infinito.
tiende a infinito.
Espero que quede más o menos claro, cualquier cosa preguntá de nuevo.
Saludos!
Como el límite en infinito es L>0, existe un real K tal a partir del cual la función es más grande que L/2 (es decir, tomando
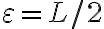 y aplicando la definición de límite).
y aplicando la definición de límite).Entonces, si querés podés partir la
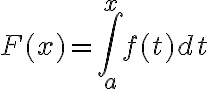 como la siguiente suma:
como la siguiente suma: 
La primera integral es un número, una constante
 , y usando que
, y usando que  es más grande que
es más grande que 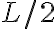 en la segunda integral, podés acotar
en la segunda integral, podés acotar 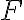 por algo como
por algo como  , y por lo tanto no puede tener límite finito cuando
, y por lo tanto no puede tener límite finito cuando  tiende a infinito.
tiende a infinito.Espero que quede más o menos claro, cualquier cosa preguntá de nuevo.
Saludos!
