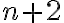CDIVV-2S: ejercicio 1f

Buenas tardes, tengo un par de dudas sobre la solución del ejercicio:

Primero, ¿la última parte de la igualdad

$( - \frac{1}{2(n+1)} + \frac{1}{2(n+2)} ) + (\frac{3}{2(n+2)} - \frac{3}{2(n+3)} )$ se escribe así por conveniencia para que luego

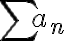$\sum a_n$ se pueda escribir como suma de dos series telescópicas?
Tampoco entendí lo último

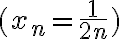$(x_n = \frac{1}{2n} )$ , capaz es simplemente una forma de llamar así a las soluciones para hacer más compacta la notación

Re: ejercicio 1f

de Leandro Bentancur - martes, 5 de septiembre de 2023, 14:19

Hola Alexis,

A la primera pregunta: exacto. Separamos el término que tiene $n+2$ en el denominador como suma de dos términos para poder escribir las dos telescópicas.

Sobre la segunda: también es correcto. Podés escribirla parecida si te queda más cómoda, pero en definitiva es lo mismo.

Saludos,

Leandro