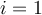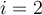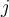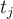Buenas, no se me ocurre cual podria ser la solucion optima. Lo que pense yo es que no importa como ordene los tiempos de natacion esa etapa siempre dura lo mismo ya que deben ir uno a la vez, por lo que tendria que ordenar el tiempo de las etapas de ciclismo y carrera a pie para que sea lo mas corto posible. El problema es que no se bien que estrategia usar porque no lo puedo comparar a los problemas del libro.
En si creo que para cada tramo tenemos su duracion y tambien cuanto tiempo despues del tramo anterior debe empezar. Entonces el tiempo que empieza el primer tramo es n1, el segundo n1+n2 , el tercero n1+n2+n3, ..etc, y el tiempo de llegada es n1+c1+p1 el del segundo es n1+n2+c2+p2 etc, por lo que el ultimo en salir llega en tiempo n1+n2+....+nm+cm+pm. Pero no puedo avanzar mas que eso. No se como ordenarlos. Alguna ayuda? Gracias