practico 4, ejercicio 1.a

practico 4, ejercicio 1.a

de Lorena Paola Rodriguez Lasarte -
Número de respuestas: 3

Buenas tardes, estaba teniendo problemas al momento de elegir como demostrar lo que me piden, ya que tengo un par de ideas pero no se si alguna de ellas es útil para esto, así que quería saber si alguna de ellas esta en el camino correcto y/o como puedo hacer para seguir.

Intentando usar la sugerencia, al principio se me ocurrió intentar hacer una especie de absurdo suponiendo que 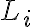 L_i contiene mas de un nodo y llegar a que solo puede contener un solo nodo, sin embargo no se me ocurre ningún motivo particular por el cual podría afirmar esto. 

También pensé en usar las componentes conexas de s y t que se forman al correr bfs desde s y t respectivamente y de algún modo ver que estas componentes están conectadas por un solo nodo en determinada capa del algoritmo a distancia 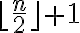\lfloor \frac{n}{2} \rfloor +1 . O incluso separar en casos sobre si es un DAG o no y analizar la secuencia de nodos desde s hasta t, pero no se me ocurre como concluir algo.

Disculpen las molestias, 

Lorena 
En respuesta a Lorena Paola Rodriguez Lasarte

Re: practico 4, ejercicio 1.a

de Facundo Benavides -
hola lorena,
comenzando por la idea de seguir nuestra sugerencia. la idea del absurdo no está mal. la justificación viene de hacer cuentas para demostrar que no es posible que todos los niveles intermedios entre s y t tengan al menos 2 nodos (más de 1 nodo) porque de ser cierto se superaría la cantidad de nodos totales 'n'.
dicho esto, la prueba no termina ahí. probar que efectivamente hay un nivel Li que contiene un único nodo 'v' es un resultado intermedio para probar que existe un equipo que si se retira desconecta 's' de 't'. precisamente, una forma de usar este resultado es reflexionar sobre las propiedades de la recorrida BFS (en particular 3.4) para ver que eliminando 'v' desconectamos a 's' de 't'.
finalmente, hago notar que el nodo 'v' está a distancia i, 1<=i<=⌊𝑛/2⌋ y que la condición de DAG no aporta.
saludos
En respuesta a Facundo Benavides

Re: practico 4, ejercicio 1.a

de Alejandro Sena Peraza -
No entiendo la ultima parte sobre lo de las propiedades de BFS, no se me ocurre como relacionar ambas cosas. No usé BFS en primer lugar para probarlo pero asumiento que empiece por decir que este camino sale en la recorrida bfs por ser de largo minimo o algo asi, como me ayuda esto?
En mi caso primero descarté que hubiera un camino alternativo totalmente independiente salvo por el inicio y el fin dada la cantidad de nodos que quedan para armarlo (seria absurdo porque seria mas corto que el mas corto que tengo). Luego hice algo parecido a la sugerencia diciendo que para evitar que se corte la conexión debería haber un nodo extra en una capa i que agregue redundancia, esto es que conecte al nodo del camino de la capa i-1 y al siguiente de la i+1 de forma que si quito el nodo del camino s-t este otro garantice conectividad, pero para cubrir un camino de largo al menos ⌊𝑛/2⌋ +1 no me alcanzan los a lo sumo ⌊𝑛/2⌋ -2 nodos que tengo por lo que va a existir un nivel el cual al quitar el nodo desconecta el camino
En respuesta a Alejandro Sena Peraza

Re: practico 4, ejercicio 1.a

de Facundo Benavides -

hola Alejandro, si descartaste que hubiese un camino alternativo (porque sería más corto) entonces todos los caminos pasan por el nodo de la capa Lh que lo contiene y por tanto al eliminarlo se desconectaría s de t.

la alternativa (análoga) a probar que no hay caminos alternativos sería usar la propiedad 3.4 para mostrar que los nodos de las capas anterior (L_h-1) y siguiente (L_h+1) a L_h no se pueden conectar directamente y por tanto, si eliminamos ese único nodo de la capa L_h desconectamos s de t.

saludos