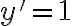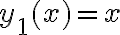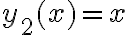Buenas, quería saber por qué esta afirmación sería falsa, tengo entendido que esto si se cumpliría para las ecuaciones lineales de primer orden ( tanto homogéneas como no homogéneas), supongo que esto no se cumple para las de segundo orden pero no estaría entendiendo por qué.