Hola, en este ejercicio yo tome como que la L1= longitud de onda 1/2 y lo mismo para L2 pero con la longitud de onda de 2. Pero no entiendo como relacionar eso con las características que tiene que tener cada una de las cuerdas. También plantee la velocidad en ambas cuerdas y supuse que la tension era igual a el peso para mantenercal cubo.
Hola, llegue a la expresión de la parte a, en la parte b no entiendo como calcular la frecuencia, tendria que agarrar una de las expresiones de la frecuencia que conseguí? Si es asi, en que momento uso el dato de la seccion transversal? Gracias
Buenas, por lo que vi hay que evaluar con los datos dados n1/n2 o n2/n1 y agarrar dos números que cumplan esa relación, para luego sustituirlos en la ecuación de la frecuencia, la densidad lineal de masa es la sección por la densidad que te dan ellos. Mi pregunta es: por que esto cumple que la frecuencia de excitación es lo mas baja posible?
Hola Ayelén y Diego.
Primero, hay que tener en cuenta que las densidades dadas tienen dimensión de masa/volumen (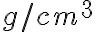
), por lo tanto se trata de densidades volumétricas (
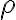). La densidad que aparece en la expresión de la velocidad de propagación de la onda es una densidad lineal (pueden hacer el análisis dimensional de la expresión para convencerse). Mirando las dimensiones de la densidad lineal y la volumétrica, vemos que hay que multiplicar la densidad volumétrica por un área para obtener las dimensiones de la densidad lineal de masa. Ahí es que juega un rol el área 
de la sección transversal: 
.
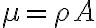Teniendo en cuenta que la secciones de los dos alambres son iguales, se llega a la relación
.
Para la parte b), con los datos dados y la expresión anterior, pueden determinar el valor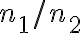
. Es importante siempre indicar qué son 
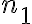y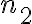 
, las expresiones que usen donde aparece un 
quedan incompletas si no indican qué representa . En este caso 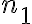y 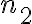en principio pueden ser 
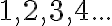. Podemos ver que la frecuencia aumenta al aumentar , dejando los otros parámetros fijos. Como nos piden hallar la mínima frecuencia de excitación, precisamos determinar los 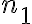y 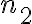enteros, más chicos posibles, que cumplan con el valor de 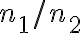que determinamos. Entonces no son dos números cualquiera, son enteros y son los más chicos posibles. Si 
, 
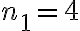y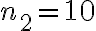 
cumplen esta relación, pero no son los enteros más chicos que la cumplen, estos serían 
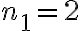y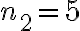 
. Una vez obtenidos los modos de vibración () de cada alambre, se puede usar la expresión de la frecuencia para obtener su valor.
Espero que esto aclare sus dudas.
Saludos.
Primero, hay que tener en cuenta que las densidades dadas tienen dimensión de masa/volumen (
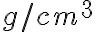), por lo tanto se trata de densidades volumétricas (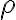). La densidad que aparece en la expresión de la velocidad de propagación de la onda es una densidad lineal (pueden hacer el análisis dimensional de la expresión para convencerse). Mirando las dimensiones de la densidad lineal y la volumétrica, vemos que hay que multiplicar la densidad volumétrica por un área para obtener las dimensiones de la densidad lineal de masa. 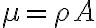Ahí es que juega un rol el área de la sección transversal: .Teniendo en cuenta que la secciones de los dos alambres son iguales, se llega a la relación
.Para la parte b), con los datos dados y la expresión anterior, pueden determinar el valor
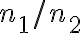. Es importante siempre indicar qué son 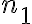y 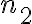, las expresiones que usen donde aparece un quedan incompletas si no indican qué representa . En este caso 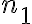y 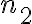en principio pueden ser 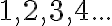. Podemos ver que la frecuencia aumenta al aumentar , dejando los otros parámetros fijos. Como nos piden hallar la mínima frecuencia de excitación, precisamos determinar los 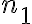y 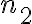enteros, más chicos posibles, que cumplan con el valor de 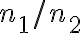que determinamos. Entonces no son dos números cualquiera, son enteros y son los más chicos posibles. Si , 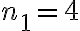y 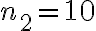cumplen esta relación, pero no son los enteros más chicos que la cumplen, estos serían 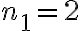y 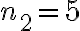. Una vez obtenidos los modos de vibración () de cada alambre, se puede usar la expresión de la frecuencia para obtener su valor.Espero que esto aclare sus dudas.
Saludos.