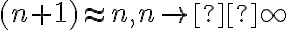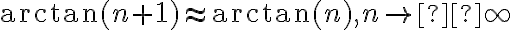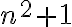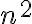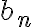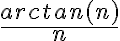Ejercicio 1-g

Ejercicio 1-g

de Alexis Sokorov Vargas -
Número de respuestas: 3

Buenas, tengo dudas sobre cómo plantear la divergencia y a qué diverge la siguiente serie:


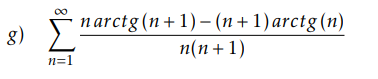
Primero evalué si podría tener chances de converger evaluando 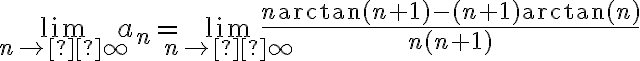 \lim_{n\to  \infty } a_n = \lim_{n\to  \infty } \frac{n \arctan(n+1) - (n+1)\arctan(n)}{n(n+1)}

supuse dos cosas:

1)  (n+1) \approx n, n \rightarrow  \infty

2)  \arctan(n+1) \approx \arctan(n) , n \rightarrow  \infty

Entonces me queda: 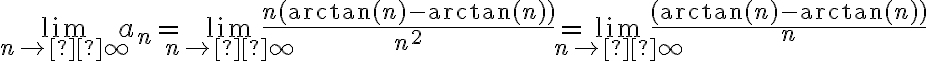 \lim_{n\to  \infty } a_n = \lim_{n\to  \infty } \frac{ n(\arctan(n) - \arctan(n))}{n^2} =\lim_{n\to  \infty } \frac{ (\arctan(n) - \arctan(n))}{n} aunque no sé si sea cero eso o si siquiera está bien razonado. En las soluciones aparece que la serie sí converge, a 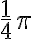\frac{1}{4} \pi, entonces  \lim de a_n tiene que darme 0
En respuesta a Alexis Sokorov Vargas

Re: Ejercicio 1-g

de Leandro Bentancur -
Hola Alexis,

Es correcto que el término general tiende a 0 pero hay que tener cuidado cuando resolvemos esas indeterminaciones. Para darte un ejemplo, n^2+1 y n^2 son equivalentes con n tendiendo a infinito pero sin embargo el límite de la resta es 1 y no 0.
Para calcular el valor de la serie te sugiero buscar la forma de escribirla como una telescópica.

Saludos,
Leandro
En respuesta a Leandro Bentancur

Re: Ejercicio 1-g

de Manuel Arrillaga D Amico -

Buenas tardes, una vez concluimos que es convergente, me está costando encontrarle la vuelta para poder resolverlo como una telescópica. Separe en dos sumandos para llevarlo a una forma de gif.latex?a_%7Bn%7D%3Db_%7Bn+1%7D-b_%7Bn%7D

Adjunto foto:


Como se seguiría??? 

En respuesta a Manuel Arrillaga D Amico

Re: Ejercicio 1-g

de Leandro Bentancur -
Hola Manuel, la última igualdad no es correcta. Supongo quisiste reordenar los términos de la suma nomás, pero intercambiaste los denominadores de los sumandos. Ahí ya tenías que tu sucesión b_n es \frac{arctan(n)}{n}.