Series - Criterio de equivalencia (Prop. 2.40)

Series - Criterio de equivalencia (Prop. 2.40)

de Alexis Sokorov Vargas -
Número de respuestas: 3

Buenas noches, tengo una duda sobre lo siguiente:


No logro visualizar el punto 2  ( \lim \frac{a_n}{b_n}=0 ) 

¿Es implícito que  b_n > a_n ? ¿Por eso da 0 el \lim ? 
En respuesta a Alexis Sokorov Vargas

Re: Series - Criterio de equivalencia (Prop. 2.40)

de Marcelo Fiori -
Hola Alexis,
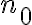no está implícito que b_n > a_n, sino que es una consecuencia de que el límite de ese cociente sea cero. Específicamente, como ese límite es cero, entonces a partir de cierto n_0 se cumple que 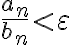\frac{a_n}{b_n} < \varepsilon (directamente usando la definición de límite). Entonces tenemos que 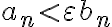a_n < \varepsilon b_n, y podemos usar el criterio de comparación (la constante 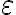\varepsilon no molesta)

Saludos!
Marcelo
En respuesta a Marcelo Fiori

Re: Series - Criterio de equivalencia (Prop. 2.40)

de Nara Martinez Brescia -
Buenas! Una consulta, si el limite del cociente es infinito entonces las series también son de la misma clase? (No me queda claro si al referirse a L se trata unicamente de un número real o si aplica para el infinito)
Gracias!
En respuesta a Nara Martinez Brescia

Re: Series - Criterio de equivalencia (Prop. 2.40)

de Marcelo Fiori -
Hola Nara,
no, en el L>0 queda implícito que tiene que ser un número finito (no estaría mal agregarlo igual).
Fijate que si el límite da infinito, entonces podés considerar el cociente inverso (cambiando de roles las sucesiones digamos) y caés en el caso de abajo, con L=0.
Saludos!