Hola Franco,
Primero decirte que está buena la idea y me parece genial el intento sin ver la resolución. Como decís el "paso tenebroso" no lo podemos usar, porque esos valores no son iguales a sino que difieren por algún valor que podemos llegar a acotar. A simple vista no veo cómo arreglarlo, tal vez acotando por otra cosa esos cocientes y operando podemos llegar.
sino que difieren por algún valor que podemos llegar a acotar. A simple vista no veo cómo arreglarlo, tal vez acotando por otra cosa esos cocientes y operando podemos llegar.
De todas formas, en algún momento hay que ser más exigente con la cota que te tomás. La razón es la siguiente, imaginemos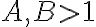 , luego
, luego 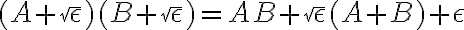 . Por lo que si estamos a
. Por lo que si estamos a 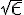 de
de  y a
y a 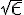 de
de  , en el producto le erramos por
, en el producto le erramos por 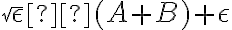 a
a 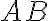 . Si
. Si 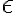 es muy chico entonces
es muy chico entonces 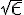 es bastante mayor (tiene la mitad de dígitos luego de la coma si lo pensamos en décimal), por lo tanto le estamos "errando" a
es bastante mayor (tiene la mitad de dígitos luego de la coma si lo pensamos en décimal), por lo tanto le estamos "errando" a 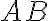 por un más de lo que queremos. Para ejemplificar podés pensar valores concretos, tomar las sucesiones iguales
por un más de lo que queremos. Para ejemplificar podés pensar valores concretos, tomar las sucesiones iguales 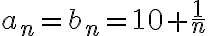 , tomar
, tomar 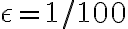 (por lo tanto
(por lo tanto 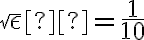 , y ver que cuando tomamos
, y ver que cuando tomamos 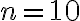 se cumple que le erramos al límite de las sucesiones por bastante más que el
se cumple que le erramos al límite de las sucesiones por bastante más que el 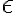 . De hecho le estamos errando por algo del orden de
. De hecho le estamos errando por algo del orden de 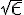 , es decir,
, es decir, 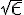 multiplicada por una constante que es
multiplicada por una constante que es 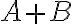 .
.
Espero se pueda seguir la respuesta, cualquier cosa consultás nomás. Largarnos a intentar probar algo y encontrarnos con una obstrucción nos ayuda a entender más que antes el problema, además de que la idea podía ser un buen punto de partida, así que me parece un buen intento de prueba.
Saludos,
Leandro
Primero decirte que está buena la idea y me parece genial el intento sin ver la resolución. Como decís el "paso tenebroso" no lo podemos usar, porque esos valores no son iguales a
 sino que difieren por algún valor que podemos llegar a acotar. A simple vista no veo cómo arreglarlo, tal vez acotando por otra cosa esos cocientes y operando podemos llegar.
sino que difieren por algún valor que podemos llegar a acotar. A simple vista no veo cómo arreglarlo, tal vez acotando por otra cosa esos cocientes y operando podemos llegar. De todas formas, en algún momento hay que ser más exigente con la cota que te tomás. La razón es la siguiente, imaginemos
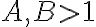 , luego
, luego 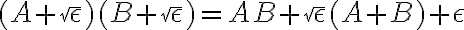 . Por lo que si estamos a
. Por lo que si estamos a 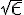 de
de  y a
y a 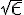 de
de  , en el producto le erramos por
, en el producto le erramos por 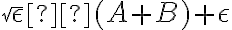 a
a 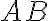 . Si
. Si 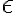 es muy chico entonces
es muy chico entonces 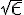 es bastante mayor (tiene la mitad de dígitos luego de la coma si lo pensamos en décimal), por lo tanto le estamos "errando" a
es bastante mayor (tiene la mitad de dígitos luego de la coma si lo pensamos en décimal), por lo tanto le estamos "errando" a 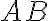 por un más de lo que queremos. Para ejemplificar podés pensar valores concretos, tomar las sucesiones iguales
por un más de lo que queremos. Para ejemplificar podés pensar valores concretos, tomar las sucesiones iguales 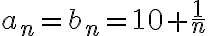 , tomar
, tomar 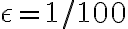 (por lo tanto
(por lo tanto 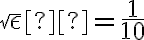 , y ver que cuando tomamos
, y ver que cuando tomamos 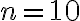 se cumple que le erramos al límite de las sucesiones por bastante más que el
se cumple que le erramos al límite de las sucesiones por bastante más que el 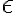 . De hecho le estamos errando por algo del orden de
. De hecho le estamos errando por algo del orden de 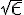 , es decir,
, es decir, 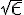 multiplicada por una constante que es
multiplicada por una constante que es 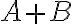 .
.Espero se pueda seguir la respuesta, cualquier cosa consultás nomás. Largarnos a intentar probar algo y encontrarnos con una obstrucción nos ayuda a entender más que antes el problema, además de que la idea podía ser un buen punto de partida, así que me parece un buen intento de prueba.
Saludos,
Leandro
