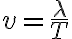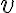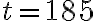Práctico 3 - Ej 2a

Práctico 3 - Ej 2a

de Alexis Sokorov Vargas -
Número de respuestas: 3

Buenas noches, tengo una duda sobre cómo hallar 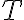T, porque lo que sé es lo siguiente: 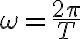\omega = \frac{2 \pi}{T} pero no tengo \omega entonces pensé poder despejarla de la ecuación general de onda 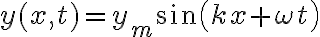y(x,t)=y_m sin(kx + \omega t) (uso + porque creo que se mueve de derecha a izquierda)

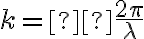Tengo k que despejé de la fórmula k =  \frac{2 \pi}{\lambda} pero no sé más cómo proseguir o si siquiera está bien encaminarlo por ese lado
En respuesta a Alexis Sokorov Vargas

Re: Práctico 3 - Ej 2a

de Roberto Elbio Peroni Martinez -
Te pide el período, que es el tiempo que demora en completar una oscilación . Para calcularlo yo usé el dato del tiempo que demora desde el máximo desplazamiento hasta el punto cero.
En respuesta a Roberto Elbio Peroni Martinez

Re: Práctico 3 - Ej 2a

de Alexis Sokorov Vargas -
No entiendo cómo relacionarlo sinceramente. Lo único que sé es v=\frac{\lambda}{T} pero no tengo v , entonces no sabría cómo usar el t (=178ms) que me dan
En respuesta a Alexis Sokorov Vargas

Re: Práctico 3 - Ej 2a

de Virginia Feldman -
Hola Alexis.
En la letra te dicen que un punto (un pequeño pedazo de la cuerda) se mueve desde su punto máximo hasta su próximo desplazamiento nulo en t=185 ms. Si seguimos observando el movimiento de ese punto en el tiempo, veremos que pasa a tener un desplazamiento y negativo, luego mínimo y depués empieza a aumentar nuevamente, pasando por un nuevo desplazamiento nulo y llegando nuevamente a su valor máximo. El tiempo entre esos dos máximos consecutivos, por los que pasa el punto, corresponde a un período. Por lo tanto, el dato que nos dan del tiempo entre el máximo y el siguiente desplazamiento nulo corresponde a cierta fracción del período. ¿Qué fracción del período representa?

A ver si por ahí sale la relación necesaria.
Saludos.