La clase pasada vimos un resultado de convergencia, que a grandes rasgos dice lo siguiente:
Si 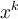 es generada mediante un método de gradiente, donde las direcciones son "gradient related", y el paso se selecciona mediante Armijo, entonces toda sub-sucesión convergente de
es generada mediante un método de gradiente, donde las direcciones son "gradient related", y el paso se selecciona mediante Armijo, entonces toda sub-sucesión convergente de 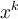 , converge a un punto estacionario de
, converge a un punto estacionario de 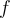 .
.
Dado que el paso es seleccionado mediante Armijo, el enunciado tiene implícito el hecho de que el paso seleccionado no sólo garantiza descenso, sino que garantiza "suficiente descenso".
Esta condición de "suficiente descenso", es necesaria para poder garantizar que las (posibles) sub-sucesiones convergentes de 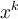 , convergen a un punto estacionario de
, convergen a un punto estacionario de 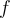 .
.
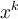 , convergen a un punto estacionario de
, convergen a un punto estacionario de 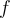 .
.Como prueba de esta afirmación, pueden ver el ejemplo que adjunto, tomado del libro de Bertsekas (capítulo 2).
Este ejemplo considera un método de gradiente, donde las direcciones son las de máximo descenso local:  . Como vimos, estas direcciones cumplen con la condición de ser gradient related. Por otro lado, el paso es seleccionado con una regla de disminución iterativa, pero que solamente exige lograr descenso. Es decir: no pide "suficiente descenso", como sí lo hace Armijo.
. Como vimos, estas direcciones cumplen con la condición de ser gradient related. Por otro lado, el paso es seleccionado con una regla de disminución iterativa, pero que solamente exige lograr descenso. Es decir: no pide "suficiente descenso", como sí lo hace Armijo.
 . Como vimos, estas direcciones cumplen con la condición de ser gradient related. Por otro lado, el paso es seleccionado con una regla de disminución iterativa, pero que solamente exige lograr descenso. Es decir: no pide "suficiente descenso", como sí lo hace Armijo.
. Como vimos, estas direcciones cumplen con la condición de ser gradient related. Por otro lado, el paso es seleccionado con una regla de disminución iterativa, pero que solamente exige lograr descenso. Es decir: no pide "suficiente descenso", como sí lo hace Armijo.Lo que se prueba entonces es que, si iniciamos en un 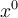 con
con  , el método genera un sucesión con dos sub-sucesiones convergentes, pero ninguna de estas converge a un punto estacionario. De nuevo: la razón por la que ocurre esto, es porque el paso seleccionado no garantiza suficiente descenso (solamente garantiza descenso).
, el método genera un sucesión con dos sub-sucesiones convergentes, pero ninguna de estas converge a un punto estacionario. De nuevo: la razón por la que ocurre esto, es porque el paso seleccionado no garantiza suficiente descenso (solamente garantiza descenso).
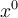 con
con  , el método genera un sucesión con dos sub-sucesiones convergentes, pero ninguna de estas converge a un punto estacionario. De nuevo: la razón por la que ocurre esto, es porque el paso seleccionado no garantiza suficiente descenso (solamente garantiza descenso).
, el método genera un sucesión con dos sub-sucesiones convergentes, pero ninguna de estas converge a un punto estacionario. De nuevo: la razón por la que ocurre esto, es porque el paso seleccionado no garantiza suficiente descenso (solamente garantiza descenso).Saludos.
Matías V.
