Buenas!
Estoy haciendo el 4 y el resultado que obtengo no es el correcto. Supongo que es un error a la hora de definir la integral, pero no veo cuál.
Gracias!
Buenas!
Estoy haciendo el 4 y el resultado que obtengo no es el correcto. Supongo que es un error a la hora de definir la integral, pero no veo cuál.
Gracias!

 es la presión a una profundidad
es la presión a una profundidad  . Esta se puede considerar constante para un área diferencial
. Esta se puede considerar constante para un área diferencial 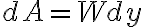 a esa profundidad. Por lo tanto, sobre esa área se obtiene un diferencial de fuerza aplicada
a esa profundidad. Por lo tanto, sobre esa área se obtiene un diferencial de fuerza aplicada 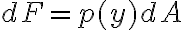 . Para obtener la fuerza total, en tu integral lo que está faltando es
. Para obtener la fuerza total, en tu integral lo que está faltando es 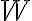 , porque solo estás integrando la presión por el diferencial de altura. Por lo que veo que pusiste, parece ser que interpretás el resultado de esa integral como una presión que luego multiplicás por el área total, esto no es correcto. Si hacés un análisis dimensional podés ver que la fuerza resultante que obtenés no tiene unidades de fuerza y el resultado de la integral no tiene unidades de presión.
, porque solo estás integrando la presión por el diferencial de altura. Por lo que veo que pusiste, parece ser que interpretás el resultado de esa integral como una presión que luego multiplicás por el área total, esto no es correcto. Si hacés un análisis dimensional podés ver que la fuerza resultante que obtenés no tiene unidades de fuerza y el resultado de la integral no tiene unidades de presión.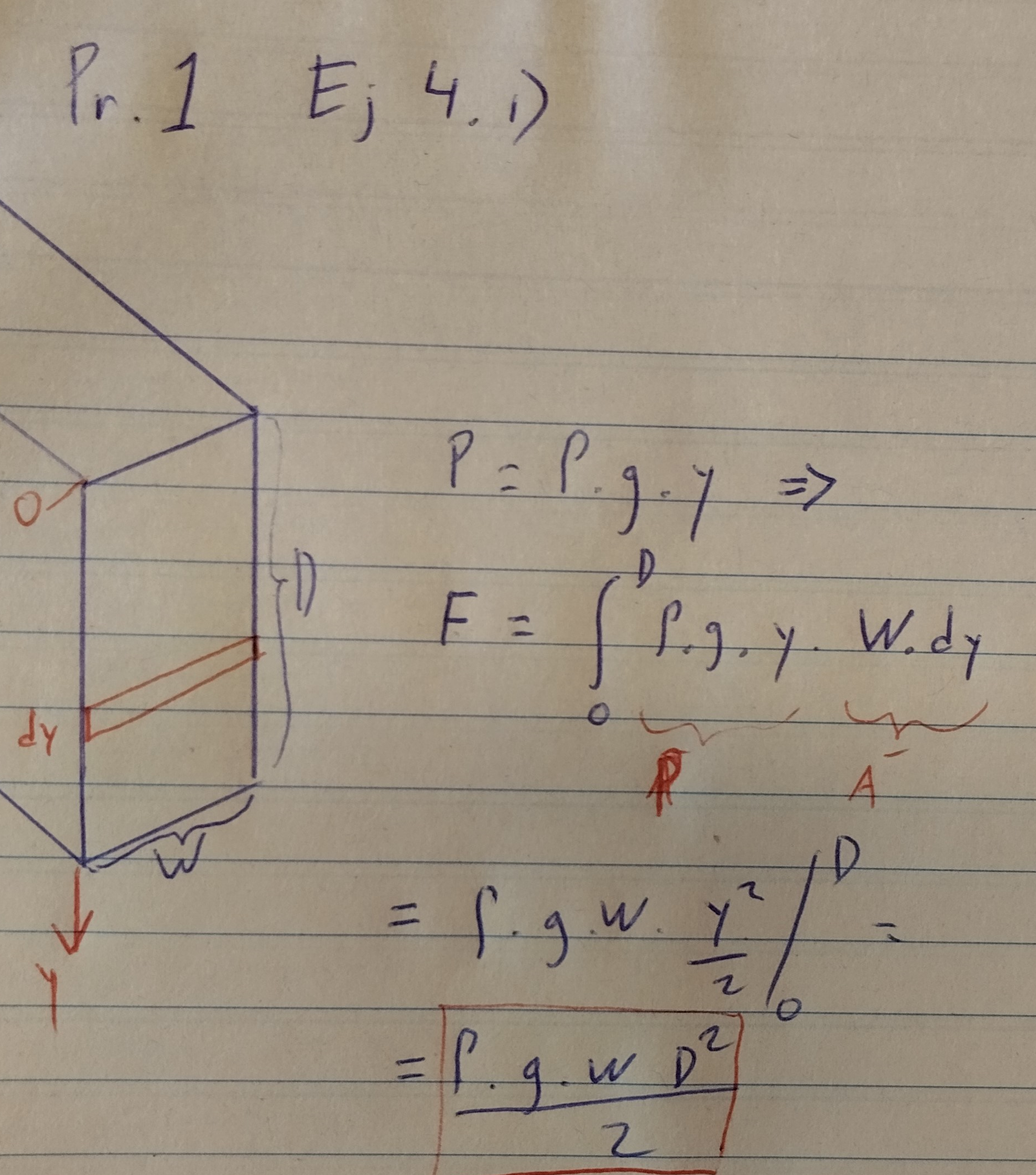
Sí, perfecto, intento.
Gracias!