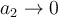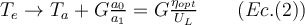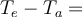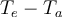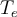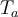Rectifico los números usando la ecuación cuadrática para la eficiencia, Ec. 2.2 (Parte 2), 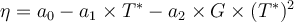 donde
donde 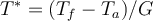 y queremos encontrar
y queremos encontrar 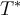 al cual
al cual 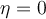 . Hay dos soluciones matemáticas, pero sabemos que
. Hay dos soluciones matemáticas, pero sabemos que 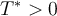 así que nos interesa la positiva. Usando la expresión usual para las raíces de una ecuación cuadrática, la raíz positiva es
así que nos interesa la positiva. Usando la expresión usual para las raíces de una ecuación cuadrática, la raíz positiva es ![T^*=\frac{a_1}{2a_2G}\left[\sqrt{1+G\frac{4a_2a_0}{a_1^2}}-1\right] T^*=\frac{a_1}{2a_2G}\left[\sqrt{1+G\frac{4a_2a_0}{a_1^2}}-1\right]](https://eva.fing.edu.uy/filter/tex/pix.php/950401809092ed45f7cb93e8d76a8597.png) (Ec. (1)) De aquí, obtenemos una temperatura de estancamiento, para el caso de eficiencia cuadrática
(Ec. (1)) De aquí, obtenemos una temperatura de estancamiento, para el caso de eficiencia cuadrática 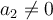 ,
,
![T_e = T_a + \frac{a_1}{2a_2}\left[\sqrt{1+G\frac{4a_2a_0}{a_1^2}}-1\right]\qquad (Ec. (1))} T_e = T_a + \frac{a_1}{2a_2}\left[\sqrt{1+G\frac{4a_2a_0}{a_1^2}}-1\right]\qquad (Ec. (1))}](https://eva.fing.edu.uy/filter/tex/pix.php/142896a9ed526824520fa216e64d0681.png)
Cuando 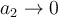 , esta expresión se reduce a (hay que recordar un poco los límites para verlo)
, esta expresión se reduce a (hay que recordar un poco los límites para verlo)
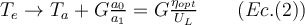
Para los valores de a0, a1 y a2 dados en la Tabla 2.1 (pag. 27, Parte 2) la Ec. (1) da 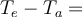 78, 116 y 150 grados Celcius para CS1, CS2 y CS3 respectivamente. Estos valores son consistentes con las Figuras 2.6 y 2.7, Parte 2 del Manual.
78, 116 y 150 grados Celcius para CS1, CS2 y CS3 respectivamente. Estos valores son consistentes con las Figuras 2.6 y 2.7, Parte 2 del Manual.
Por otro lado, si despreciamos la dependencia cuadrática de las pérdidas térmicas y usamos a2=0, y calculamos 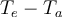 usando la Ec. (2) obtenemos 100, 200 y 375 grados Celcius respectivamente, lo cual es mayor (como hay menos pérdidas consideradas en el modelo lineal,
usando la Ec. (2) obtenemos 100, 200 y 375 grados Celcius respectivamente, lo cual es mayor (como hay menos pérdidas consideradas en el modelo lineal, 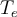 resulta mayor).
resulta mayor).
Espero ahora haya quedado más claro. La confusión generada es que en mi respuesta anterior, la eficiencia estaba parametrizadacon la Ec. (3.14) de la parte 1 (coeficienctes c0, c1, c2) y en el apuro la evalué para los coeficientes a0, a1, a2 de la Ec. (2.2), parte 2, lo cual daba números inconsistentes.
En suma, la Ec. (1) puede usarse para evaluar la temperatura de estancamiento 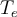 para irradiación dada G, y temperatura ambiente conocida
para irradiación dada G, y temperatura ambiente conocida 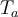 , cuando se cuenta con los coeficientes a0, a1, a2 de la parametrización cuadrática de la eficiencia del colector.
, cuando se cuenta con los coeficientes a0, a1, a2 de la parametrización cuadrática de la eficiencia del colector.
Saludos,
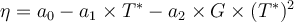
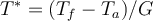
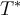
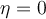
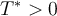
![T^*=\frac{a_1}{2a_2G}\left[\sqrt{1+G\frac{4a_2a_0}{a_1^2}}-1\right] T^*=\frac{a_1}{2a_2G}\left[\sqrt{1+G\frac{4a_2a_0}{a_1^2}}-1\right]](https://eva.fing.edu.uy/filter/tex/pix.php/950401809092ed45f7cb93e8d76a8597.png)
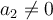
![T_e = T_a + \frac{a_1}{2a_2}\left[\sqrt{1+G\frac{4a_2a_0}{a_1^2}}-1\right]\qquad (Ec. (1))} T_e = T_a + \frac{a_1}{2a_2}\left[\sqrt{1+G\frac{4a_2a_0}{a_1^2}}-1\right]\qquad (Ec. (1))}](https://eva.fing.edu.uy/filter/tex/pix.php/142896a9ed526824520fa216e64d0681.png)