Hola, tengo una duda sobre si esta función es derivable en 0 o no. Planteé el cociente incremental y me queda que el límite de f(x) cuando x tiende a 0 es 0 y que el límite 1/x cuando x tiende a 0 no existe, por lo tanto, seria 0. no existe y eso nos da 0? eso nos estaría diciendo que f(x) es derivable en 0? Gracias
Buenas
Lo que comentas pasa siempre que plantees el cociente incremental en una funcion continua, es decir  cuando
cuando 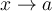 y
y 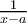 no existe cuando
no existe cuando 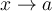 (aunque se pueden estudiar los limites laterales para ver que son
(aunque se pueden estudiar los limites laterales para ver que son  ). En otras palabras siempre es una indeterminación (si
). En otras palabras siempre es una indeterminación (si  es continua)
es continua)
En este caso la idea es plantar el cociente incremental por limite laterales ay que hay una funcion valor absoluto en la función 
Por tanto no existe la derivada.
Si calculas el limite lateral en  obtendras
obtendras 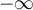
Saludos

