Buenas
Debes recordar que cuando buscas primitivas de 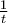 lo que obtienes es
lo que obtienes es  , es deciur aparece un valor absoluto. Puedes pasarlo a tu caso (
, es deciur aparece un valor absoluto. Puedes pasarlo a tu caso ( ) de forma análoga.
) de forma análoga.
Voy a comentar en algunos ejemplos para que se vea mejor
Si tuvieras que el intervalo de integracion tiene tanto valores negativos como postivos no pòdrias realizar la integral (como vemos en este curso), pues la funcion no esta acotada
 . En este caso no se puede calcular la itnegral por que
. En este caso no se puede calcular la itnegral por que 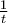 no esta acotada en
no esta acotada en ![[-1,2] [-1,2]](https://eva.fing.edu.uy/filter/tex/pix.php/939b17134a44bb821e6c01efd044b32e.png) .
.
En el caso que todo el intervalo sea negativo si cobra importancia el valor absoluto
Si queires verificar esta igualdad, puedes realizar un cambio de variable t = -v, y en ese caso el intervalo queda dentro de los positivos, mas precisamente
Cualqueir cosa vuelve a escribir
Saludos


