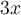CDIV-1S: Examen 2020 Vespertino - Ejercicio 5

Hola buenas tardes!

No logro reslever el ejercicio, dudo que sea aplicando l'hopital sin relover algo antes, debido a que se hace demasiado extenso y tardado, entiendo que a tan(x) lo piuedo esxpresar como sen(x)/(cos(x) pero no comprendo si puedo realizar algun timpo de simplificacion del aspecto sen(u)/sen(v). Desde ya muchas gracias !

Saludos Franco!

Re: Examen 2020 Vespertino - Ejercicio 5

de Bruno Yemini - martes, 18 de julio de 2023, 11:58

Hola, es totalmente entendible lo que decís. Posiblemente te sea más económico sustituir cada expresión por su respectivo polinomio de Taylor centrado en 0.

Intentalo por ahí y nos contás.
Saludos,
Bruno

Re: Examen 2020 Vespertino - Ejercicio 5

de Alexis Sokorov Vargas - martes, 18 de julio de 2023, 14:02

Buenas, disculpa, tengo una duda sobre cómo plantearlo con Taylor: ¿hasta qué orden convendría hacerlo? Porque como en el numerador aparece log(1+2x^2)ln(1+2x2) supuse que sería de orden dos todos los polinomios. Me quedó así:

Me mareó plantear la derivada segunda de

$tan(3x)$ y supuse que, como

$tan(3x)'=\frac{3}{cos^{2}(3x)}$ entonces

$tan(3x)''$ es con

$sin$ y evaluado en 0 la derivada segunda daría cero

Re: Examen 2020 Vespertino - Ejercicio 5

de Bruno Yemini - martes, 18 de julio de 2023, 14:47

Está bien eso.

Sobre el grado de los polinomios, seguí hasta que te quede un polinomio distinto del nulo nomás. Hay formas de calcular el polinomio de Taylor con menos derivadas -más bien con derivadas menos complicadas- usando las propiedades de unicidad del polinomio de taylor.

Por ejemplo, podés calcular el polinomio (de orden 3) de

$\tan u$ ,

$\displaystyle \tan u = u + \frac{u^3}{3} + r_3(u).$

Y entonces, evaluando en

$3x$ obtenemos el polinomio

$\displaystyle \tan(3x) = 3x + \frac{{(3x)}^3}{3} + r_3(3x).$

La unicidad del polinomio de Taylor nos garantiza que el polinomio que encontrás así es el de

$\tan(3x)$ .

Lo mismo con

$\log(1+2x^2)$ , primero tomamos el polinomio (de grado dos) de

$\log(1+u)$ ,

$\displaystyle \log(1+u) = u - \frac{u^2}{2} + r_2(u).$

Evaluamos en

$u = 2x^2$ obtenemos

$\displaystyle \log(1+2x^2) = 2x^2 - \frac{{(2x^2)}^2}{2} + r_2(2x^2) = 2x^2 - 2x^4 + r_2(2x^2) = 2x^2 + \tilde{r}_2(x).$

El polinomio de Taylor de grado 2 de

$\log(1+2x^2)$ (observá que los términos de orden superior los mandé todos al resto).

Para las derivadas de la tangente, a la hora de calcular, a veces me parece mejor escribir

$\tan ' (x) = 1+\tan^2(x)$ , al no haber divisiones me parece más amigable para hacer cálculos de derivadas superiores.

Bueno, mucho texto para decir que estaba bien lo que hiciste. Perdón.

Saludos.

Re: Examen 2020 Vespertino - Ejercicio 5

de Alexis Sokorov Vargas - martes, 18 de julio de 2023, 15:53

Me parece muchísimo más sencillo lo que planteaste vos. Pero me surgió una duda más, ¿por qué cuando evaluaste los polinomios de Taylor tanto de

$tan(3x)$ como de

$log(1+2x^2)$ te quedas con los de menor grado? Es decir,

$tan(3x)=3x$ y

$log(1+2x^2)=2x^2$
O capaz viene de la mano con lo que comentaste ni bien al principio de hallar polinomios NO NULOS, por eso a la hora de resolverlo basta con que

$tan(3x)=3x$ por ejemplo, y razonando análogamente para los demás