La derivada de  en
en 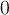 se define como el límite (en el caso de que exista):
se define como el límite (en el caso de que exista):
 .
.
Si la función está definida en un entorno de
está definida en un entorno de 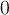 y es derivable en
y es derivable en 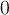 , entonces se puede cambiar
, entonces se puede cambiar  por
por 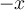 en límite y da exactamente lo mismo ya que
en límite y da exactamente lo mismo ya que  , es decir:
, es decir:

Entonces, en caso de que sea derivable en
sea derivable en 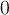 ,
,


En esta última igualdad se cancela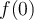 y se usa la hipótesis del ejercicio.
y se usa la hipótesis del ejercicio.
En general el límite de la definición de derivada es indeterminado del tipo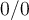 , pero esto no quiere decir que no exista.
, pero esto no quiere decir que no exista.
 en
en 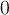 se define como el límite (en el caso de que exista):
se define como el límite (en el caso de que exista): .
.Si la función
 está definida en un entorno de
está definida en un entorno de 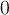 y es derivable en
y es derivable en 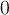 , entonces se puede cambiar
, entonces se puede cambiar  por
por 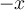 en límite y da exactamente lo mismo ya que
en límite y da exactamente lo mismo ya que  , es decir:
, es decir:
Entonces, en caso de que
 sea derivable en
sea derivable en 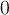 ,
, 

En esta última igualdad se cancela
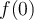 y se usa la hipótesis del ejercicio.
y se usa la hipótesis del ejercicio.En general el límite de la definición de derivada es indeterminado del tipo
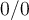 , pero esto no quiere decir que no exista.
, pero esto no quiere decir que no exista.