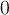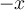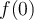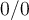Hola, en este ejercicio no entiendo bien la resolución. Plantea la definición de derivada en xo=0 para x y -x y toma como que son iguales las derivadas en ese punto? porque si es asi, no sería indeterminado el limite planteado en la letra del ejercicio? porque sería 0/0
Otra cosa que no me quedo claro es por que la suma de las derivadas de x y -x dan el limite planteado en la letra
Gracias