Buenas, en este problema asumo que al tocar los pistones, el trabajo realizado por el gas es 0. Ésto porque? Como me doy cuenta? Gracias

Buenas, en este problema asumo que al tocar los pistones, el trabajo realizado por el gas es 0. Ésto porque? Como me doy cuenta? Gracias

Hola, primero que nada hay que calcular el intercambio de calor. Si el piston se comprime significa que la temperatura del gas disminuyó. Todo el calor perdido por el gas es el ganado por el hielo.
Tenemos que el 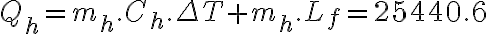 donde
donde 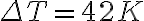 . Todo el calor ganado por el hielo es el calor perdido por el gas, entonces
. Todo el calor ganado por el hielo es el calor perdido por el gas, entonces 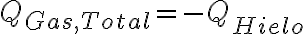
Claramente hay tres estados y dos procesos, una compresión a 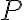 ctte(1-2) y una presurización a
ctte(1-2) y una presurización a 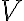 ctte(2-3). Los tres estados son inicial(1), justo cuado toca los soportes(2) y final(3)
ctte(2-3). Los tres estados son inicial(1), justo cuado toca los soportes(2) y final(3)
Podemos calcularnos el trabajo en el proceso 1-2 con 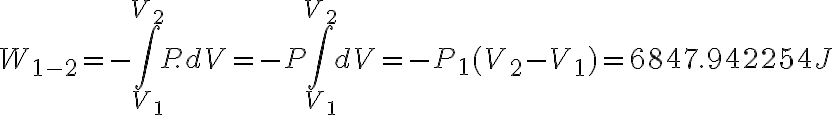 . En el proceso 2-3 no hay trabajo porque no hay cambio de volumen, entonces
. En el proceso 2-3 no hay trabajo porque no hay cambio de volumen, entonces 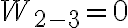 . Podes convencerte pensando en el diagrama PV, el trabajo es el área debajo de la curva que describe un proceso, una presurización a
. Podes convencerte pensando en el diagrama PV, el trabajo es el área debajo de la curva que describe un proceso, una presurización a 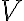 ctte es una recta vertical, entonces no hay área bajo esa recta.
ctte es una recta vertical, entonces no hay área bajo esa recta.
Podemos calcular el 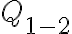 con
con 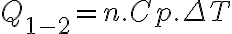 ,
, 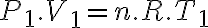 y
y 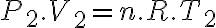 . Resto estas dos ecuaciones de estado y me queda
. Resto estas dos ecuaciones de estado y me queda 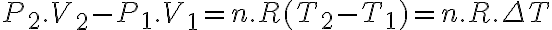 . Sabemos que
. Sabemos que 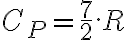 entonces nos queda
entonces nos queda 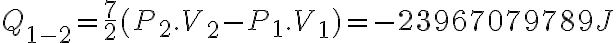
Ya tenemos 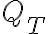 y
y 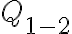 , podemos calcular el que nos falta con
, podemos calcular el que nos falta con 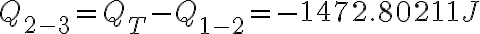 . Con eso ahora podemos obtener la presión final.
. Con eso ahora podemos obtener la presión final.
El 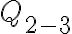 se puede calcular usando
se puede calcular usando 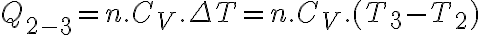 Sabemos que
Sabemos que  entonces de la ecuación de estado podemos despejar la temperatura y nos queda
entonces de la ecuación de estado podemos despejar la temperatura y nos queda 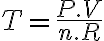 . Insetamos esto en la otra ecuación y obtenemos
. Insetamos esto en la otra ecuación y obtenemos 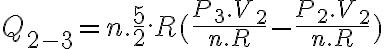 . Sabemos todo de ahí menos la presión final, y si la despejamos obtenemos
. Sabemos todo de ahí menos la presión final, y si la despejamos obtenemos 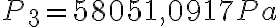
Te dejo el resto para vos, espero que se halla entendido el razonamiento. Si no decime y vemos
El gran tema con usar la ecuación de estado como vos sugerís es que siempre tenemos 2 incógnitas, en ningún momento obtuvimos la cantidad de moles. Según el planteo que yo hice tampoco necesitamos calcular las temperaturas del estado 1 ni del 2.
Estuve tremendo rato pensando en una manera de conseguir 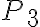 como vos sugerís, masajeando las ecuaciones a ver si aparece algo y no me sale. Si hay una manera no se me ocurre cómo, seguro la letra del ejercicio fue diseñada para que el estudiante deba conseguir estos datos de la forma en que yo lo plantié o una similar.
como vos sugerís, masajeando las ecuaciones a ver si aparece algo y no me sale. Si hay una manera no se me ocurre cómo, seguro la letra del ejercicio fue diseñada para que el estudiante deba conseguir estos datos de la forma en que yo lo plantié o una similar.
Ojo, ahora que tenes 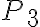 podes despejar
podes despejar  , y ya teniendo
, y ya teniendo  podes conseguir
podes conseguir 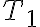 y
y 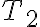 .
.  te va a ser necesario para calcular la entropía.
te va a ser necesario para calcular la entropía.