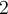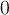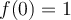Buenas tengo una pregunta con el ejercicio 4 del VoF

La respuesta es verdadero, pero si derivo usando el TFC me queda que la derivada es siempre positiva, no sería un Punto de inflexión en lugar de un mínimo?
o quizas haya que estudiar el límite cuando x tiende a 0 de la derivada.
También tengo una pregunta con la siguiente solucion del parcial MO.
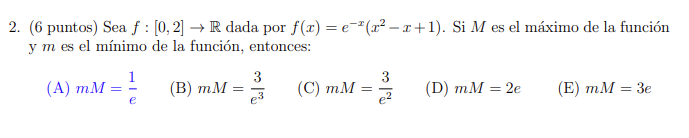
Me da que es la B, hay un error en la solución?
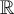
![[0,2\pi] [0,2\pi]](https://eva.fing.edu.uy/filter/tex/pix.php/1cc5fb6d3b10cf0b4029e23d46fa7fc0.png)


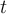
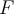
![[a,b] [a,b]](https://eva.fing.edu.uy/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.png)