
Hola, ya hallamos la primitiva de f(x) pero no entendemos a que se refiere cuando dice "determinar los intervalos maximales donde está definida" A qué se refiere y cómo se hallarían?
Tampoco se nos ocurre como resolver la 2.

Hola, ya hallamos la primitiva de f(x) pero no entendemos a que se refiere cuando dice "determinar los intervalos maximales donde está definida" A qué se refiere y cómo se hallarían?
Tampoco se nos ocurre como resolver la 2.
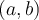 que verifica algo -en este caso el intervalo donde la primitiva está definida- es maximal (para ese algo) si otro intervalo
que verifica algo -en este caso el intervalo donde la primitiva está definida- es maximal (para ese algo) si otro intervalo 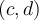 que donde la primitiva esté definida cumple
que donde la primitiva esté definida cumple  entonces
entonces  . En definitiva, te está pidiendo los intervalos más grandes donde la primitiva de
. En definitiva, te está pidiendo los intervalos más grandes donde la primitiva de  está definida. Como ya hallaron
está definida. Como ya hallaron  sólo tienen que buscar los intervalos más grandes donde
sólo tienen que buscar los intervalos más grandes donde  tiene sentido.
tiene sentido.
Hola! Te respondo primero lo de la parte 2. El procedimiento que usaste está perfecto, no tiene que entrar ningún logatirmo. El tema es que hay algunos errores de cuenta:
Primero, se te pasó por alto un 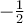 que venía del cambio de variable. Considerando eso, la primitiva termina quedando
que venía del cambio de variable. Considerando eso, la primitiva termina quedando  .
.
Después por otra parte, cos(0)=1, por lo tanto arcos(1)=0. Aplicando Barrow queda lo siguiente:
Fijate que los términos de arcos se anulan ambos. El primero porque arcos(1)=0 y el segundo porque está multiplicado por 0.
 que están integrando se va a infinito en algunos puntos (en las raíces del denominador). En esos puntos la primitiva no tiene sentido. No me fijé cuales son exactamente esos puntos, pero ponele que si fueran -1 y 2, entonces los intervalos maximales en que la primitiva está definida supongo que serían (-inf,-1), (-1,2) y (2,inf). Si ya calcularon la primitiva pueden fijarse dónde está definida. Supongo que los únicos puntos en los que la primitiva no estaría definida son los puntos en los que
que están integrando se va a infinito en algunos puntos (en las raíces del denominador). En esos puntos la primitiva no tiene sentido. No me fijé cuales son exactamente esos puntos, pero ponele que si fueran -1 y 2, entonces los intervalos maximales en que la primitiva está definida supongo que serían (-inf,-1), (-1,2) y (2,inf). Si ya calcularon la primitiva pueden fijarse dónde está definida. Supongo que los únicos puntos en los que la primitiva no estaría definida son los puntos en los que  tampoco está definida.
tampoco está definida.