Ejercicio 4 Parte a

Ejercicio 4 Parte a

de Diego Ismael Marichal Chavez -
Número de respuestas: 1

Hola, no entiendo porque se cumple 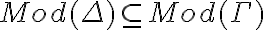Mod(\Delta) \subseteq Mod(\Gamma)

Mod(\Delta) = \{ M : M \models \Delta \} 

Entonces por 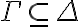\Gamma \subseteq \Delta en particular para las mismas estructuras o menos estructuras(ya que si 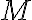M modela 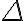\Delta tiene que poder modelar \Gamma) 

\{ M : M \models \Gamma \} = Mod(\Gamma)

Entonces Mod(\Gamma) \subseteq Mod(\Delta)

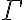No entiendo porque este razonamiento estaria mal

Saludos

Diego
En respuesta a Diego Ismael Marichal Chavez

Re: Ejercicio 4 Parte a

de Guillermo Calderon - InCo -

Buenas:

Es correcto esto que decís:

" ... si M modela Δ tiene que [poder] modelar Γ"

Esto significa que:

  • Todo modelo de Δ es modelo de Γ

Lo que equivale a:

  • M ⊧ Δ ⇒ M ⊧ Γ

Que a su vez es lo mismo que:

  • M ∈ MOD(Δ) ⇒ M ∈ MOD(Γ)

Y de ahí surge la inclusión:

  • MOD(Δ) ⊆ MOD(Γ)