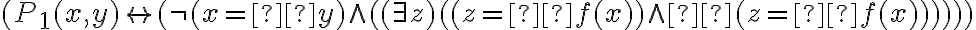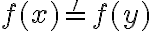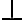Que tal Diego:
Tu definición de hermanos tiene un pequeño error (posiblemente error al transcribir). Hay una  al final que debería ser
al final que debería ser  .
.
Esa definición de hermanos se puede hacer más simple: se puede
decir directamente que 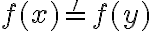 sin necesidad del
sin necesidad del  .
.
Supongo que escribiste la irreflexiva en FORM. ¿cómo quedó?
La idea es probar que ninguna persona cumple ser hermano de sí mismo.
Esto se deriva directamente de la definición de hermanos que
dice que deben ser distintos.
Informalmente el razonamiento es:
- supongo que x es hermano de x
- concluyo que no se cumple x = x
- lo anterior se contradice con la reflexiva de la igualdad (RI1)
- llegamos a una contradicción (
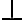 )
)
- se concluye que no es cierto que x es hermano de x
Esta idea se debe escribir como una derivación.
Si algo no queda claro, volvé a preguntar.