¿El versor normal no debería ser colineal con la derivada segunda de alfa? Es decir, ¿puedo hallarlo con la derivada segunda de alfa dividido su norma? Pregunto porque en el práctico dos aparece como el producto vectorial de la derivada primera con la segunda y el resultante con la primera, lo que me da a entender, que es el sentido y dirección de la derivada segunda...
No necesariamente la aceleración es perpendicular a la velocidad (que sería lo que preguntas). Fijate por ejemplo en la parabola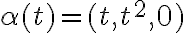 
Tenés que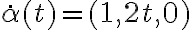 
y 
y 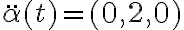su producto escalar entonces es 4t, distinto de cero para todo $t \neq 0$. O sea, en casi todos los puntos de 
la aceleración no es perpendicular a la velocidad.
Lo que sí suele pasar (y es en cierta forma, con lo que se cuenta en las definiciones esas) es que la aceleración no es colineal con la velocidad (igual está bueno ver qué pasa cuando sí lo es), que no sean colineales implica que determinan un plano. La normal está en ese plano.
Al tener que el producto cuña (o vectorial) da vectores perpendiculares a los interiores, tenés que la binormal es perpendicular al plano determinado por la aceleración y la velocidad (y por lo tanto, perpendicular a estas dos), y la normal es perpendicular al plano determinado por la velocidad y la binormal, esta dirección no necesariamente contiene a la aceleración. Lo que podés hacer para convencerte de esto es tratar de buscar el ángulo de la normal de la parábola que te dí arriba con la aceleración.
Un abrazo