Ejercicio 10 - a.II

Ejercicio 10 - a.II

de Anthony Matias Cuña Silveira -
Número de respuestas: 3

Buenas, para probar esta parte del ejercicio, en la guía recomiendan demostrar dos cosas, y una de ellas es que  \models \varphi \ \Rightarrow \ \models (\forall x) \varphi . Intente hacer esto pero no sé si es correcto el cómo lo hice:

Como \models \varphi, entonces por definición de \models, (\stackrel{\mathrm{\_}}{\forall} M:eta) M \models \varphi, considerando M arbitrario, ¿es correcta la siguiente afirmación: "Si M \models \varphi entonces (\stackrel{\mathrm{\_}}{\forall} a\in |M|)M \models \varphi[\stackrel{\mathrm{\_}}{a}/x]"? 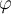Yo entiendo que esto si se cumple, debido a que lo que se está haciendo es sustituir las ocurrencias libres de x por a en \varphi y lo que se obtendría es una fórmula que también la modela cualquier M, porque cualquier M modela a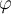 \varphi

Luego por aplicación del lema 2.4.5. se puede llegar a que \models (\forall x) \varphi, pero no sé si es correcta la afirmación antes dicha. 
En respuesta a Anthony Matias Cuña Silveira

Re: Ejercicio 10 - a.II

de Guillermo Calderon - InCo -

¿es correcta la siguiente afirmación: "Si M \models \varphi entonces (\bar\forall a \in |M|) M \models \varphi[\bar a/x]?

La afirmación es correcta pero hay que demostrarla. No surge de la aplicación de 2.4.5 puesto que \varphi puede tener otras variables libres además de x.

Es necesario considerar la clausura de \varphi para poder aplicar la definición de \models.
En respuesta a Guillermo Calderon - InCo

Re: Ejercicio 10 - a.II

de Diego Ismael Marichal Chavez -
Buenas, no me esta quedando claro como demostrar los que que pregunta el compañero,
Como ⊨φ, entonces por definición de ⊨, (∀_M:eta)M⊨φ, considerando M arbitrario, luego aplicando la clausura (∀_M:eta)M⊨(∀z)φ con z como el vector que define la docente en el video
Pero luego de esto no se que hacer para que aparezca ∀x
Saludos
Diego
En respuesta a Diego Ismael Marichal Chavez

Re: Ejercicio 10 - a.II

de Guillermo Calderon - InCo -

Hola:

Te paso alguna sugerencia de cómo encarar esa parte:

Queremos probar:

M ⊧ φ ⇒ M ⊧ (∀x)φ

Te sugiero considerar dos casos:

Caso 1 : x ∈ FV(φ).
Caso 2 : x ∉ FV(φ)

En el caso 1, se observa que las clausuras de φ y (∀x)φ son iguales y por lo tanto tienen los mismo modelos.

En el caso 2, la x no ocurre libre en φ.

Se sugiere

  • clausurar ambas fórmulas (las clausuras no son iguales)
  • aplicar 2.4.5 a ambas por cada cuantificador universal

  • usar el hecho de que cualquier sustitución de x no afecta a la fórmula φ:

    φ[t/x] = φ

Espero que ayude, cualquier cosa volvé a preguntar.