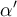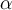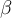Hola, tenía duda en donde está el signo de pregunta, no sé si ese P.I es 0 o el conjugado de ese P.I es 0 ya que estamos en los complejos, y si me cambia en algo. Pensé esto: Si v y w están en una bon entonces <v,w>=<w,v>=0 sin importar la tercera condición de la defunción de P.I que toma el conjugado.
Por otro lado saqué los escalares que estaban en la segunda entrada como su conjugado pero al verificar en la parte de abajo me da que está bien si no conjugo alfa y beta