A la condición de  (1) se llega en el análisis que se hace de la señal
(1) se llega en el análisis que se hace de la señal 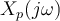 donde
donde  y
y 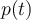 es un tren de deltas periódicas
es un tren de deltas periódicas 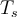 (el período de muestreo).
(el período de muestreo).
 (1) se llega en el análisis que se hace de la señal
(1) se llega en el análisis que se hace de la señal 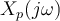 donde
donde  y
y 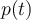 es un tren de deltas periódicas
es un tren de deltas periódicas 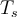 (el período de muestreo).
(el período de muestreo).En este análisis se ve que si no se cumple (1) entonces hay solapamiento entre las copias de los espectros de 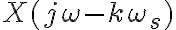 . En este análisis no hay ninguna suposición sobre cómo es la reconstrucción; luego se llega al uso del LPF (
. En este análisis no hay ninguna suposición sobre cómo es la reconstrucción; luego se llega al uso del LPF (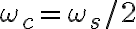 ).
).
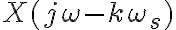 . En este análisis no hay ninguna suposición sobre cómo es la reconstrucción; luego se llega al uso del LPF (
. En este análisis no hay ninguna suposición sobre cómo es la reconstrucción; luego se llega al uso del LPF (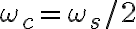 ).
).La respuesta al planteo en tu segundo párrafo surge del mismo análisis anterior. Si no se cumple (1) en las hipótesis del Teorema del Muestreo habrá solapamiento.
Puede haber casos donde se pueda violar el Teorema de Muestreo, es decir reconstruir con una frecuencia de muestreo que no cumple (1). Por ejemplo, en el Ejercicio 4 del Práctico 007. Este es un caso particular donde el análisis anterior no vale exactamente y se puede romper (1).
Si quedan más dudas, podemos verlo en más detalles en la clase de teórico/consulta del jueves.
Saludos.
