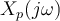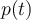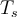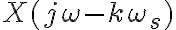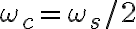Buenas.
Tengo una duda sobre el planteo del teorema de muestreo.
La condición que el teorema establece para que una señal pueda ser reconstruida a partir de sus muestras es que Ws > 2Wm, para que no haya solapamiento en el espectro de Xp(jw) y así poder recuperar X(jw) (y por tanto x(t)) al aplicar un LPF a Xp(jw).
Lo que no termino de entender es por qué es necesaria la condición de Ws > 2Wm, ya que por lo que entiendo esa condición es necesaria para recuperar x(t) por medio de un LPF. No hay forma de poder recuperar x(t) sin la necesidad de un LPF (aunque sea mas trabajoso) y de esa forma levantar la condición de Ws > 2Wm?
Por otra parte, entiendo que si no estuviese la condición de Ws > 2Wm en principio la frecuencia de muestreo podría ser cualquiera, llegando a ser tan baja que no logre muestrear la señal x(t) lo suficiente para poder reconstruirla sin grandes errores. Por lo tanto, por qué la condición sobre la frecuencia de muestreo no puede ser Ws > Wm (la cual no cumple la condición de un principio)? Esta frecuencia es mayor a la frecuencia mas grande de la señal, y por ende se estaría muestreando mas rápido de lo que la señal puede variar, posibilitando así la obtención de información suficiente para poder reconstruir x(t).
Gracias.