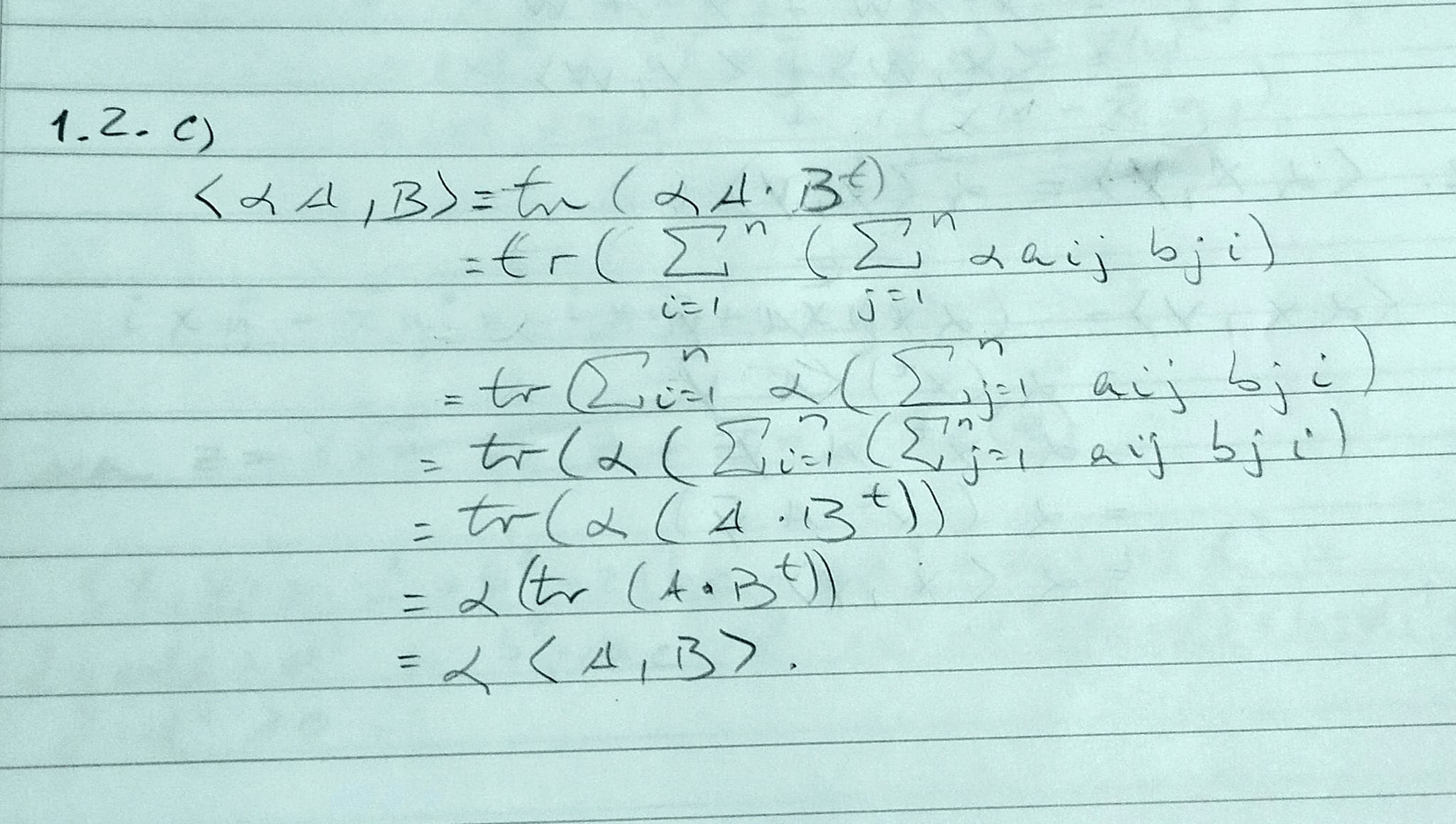Ej 1.2 (quiero probar homogeneidad)

Ej 1.2 (quiero probar homogeneidad)

de Axel Jorge Batista Infante -
Número de respuestas: 4

me definen el producto interno para el espacio de las matrices nxn(R) y quiero probar que 

<a*A,B> = traza((a*A)Bt)) = a*traza(ABt) = a<A,B> 

A,B matrices, a un escalara y Bt la matriz B traspuesta. No se como operar con a ya que no estoy seguro si (aA)Bt = a(ABt).

Espero alguien pueda ayudarme, gracias!  

En respuesta a Axel Jorge Batista Infante

Re: Ej 1.2 (quiero probar homogeneidad)

de Juan Piccini -
Hola Axel, recuerda que la traza de una matriz es la suma de los elementos de su diagonal principal, y que los elementos diagonales del producto MN se construyen tomando la fila i-sima de M, la columna i-sima de N y haciendo la suma  \sum_{j=1}^n m_{ij}n_{ji} .
Saludos
J.
En respuesta a Juan Piccini

Re: Ej 1.2 (quiero probar homogeneidad)

de Axel Jorge Batista Infante -
Entiendo, consideras esta como una prueba válida?
Adjunto yo.jpg
En respuesta a Axel Jorge Batista Infante

Re: Ej 1.2 (quiero probar homogeneidad)

de Juan Piccini -
Hay un error: al sumar los elementos diagonales ya estás calculando la traza, debes quitar "tr" luego de la segunda igualdad ya que la doble sumatoria es la traza (la sumatoria interna calcula el elemento diagonal de \alpha A B, la sumatoria externa suma dichos elementos diagonales, es la traza).
Dejando eso de lado, el resto está bien, en esencia estás probando que tr(\alpha M N)=\alpha tr(M N) .
Si llamas C=\alpha M N y D=M N, entonces C_{ii}=\sum_j\alpha M_{ij}N_{ji}=\alpha\sum_j M_{ij}N_{ji}=\alpha D_{ii}, de donde sale lo de la traza.
Saludos
J.