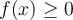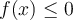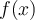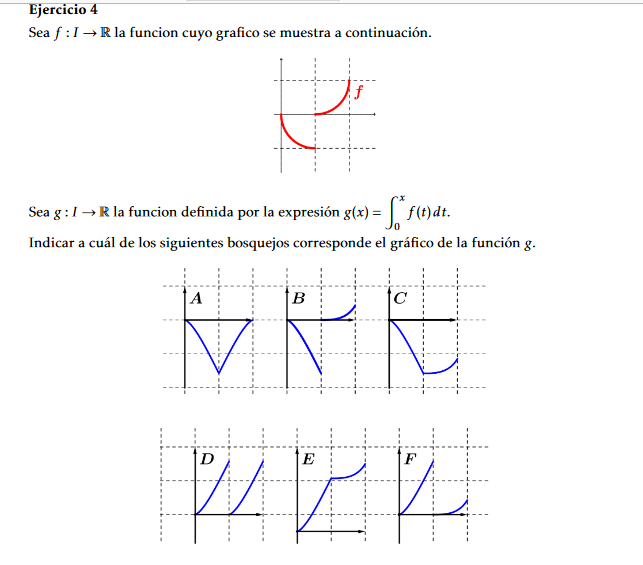
Buenas, no estaría logrando entender que la opción correcta sea la "c", con la pirmera parte de la gráfica llegué a la conclusión crrecta, pero la segunda parte de la integral no debería ser positiva al serlo su función original? no se si mi problema está en tomar f como 2 funciones distintas y por lo tanto pensar en su integral por separado, o si debería considerarlas juntas y como la sección negativa es mayor a la positiva, entonces queda toda la integral negativa.
![f:[a,b] \rightarrow \mathbb{R} f:[a,b] \rightarrow \mathbb{R}](https://eva.fing.edu.uy/filter/tex/pix.php/646efb1e019945626533a3260ddd81f7.png)
![[a,b] [a,b]](https://eva.fing.edu.uy/filter/tex/pix.php/2c3d331bc98b44e71cb2aae9edadca7e.png)
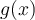

![x \in [a,b] x \in [a,b]](https://eva.fing.edu.uy/filter/tex/pix.php/af3c1adca188345d2a91c0d13a891b9f.png)