Según las soluciones, todas son correctas (opción B), pero no entiendo por qué la tercera es correcta. Tendría sentido si la función fuera continua pero no lo específica.

Según las soluciones, todas son correctas (opción B), pero no entiendo por qué la tercera es correcta. Tendría sentido si la función fuera continua pero no lo específica.

Buenas
La idea es usar la propiedad de monotonia de la integral:
Dados 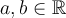 con
con 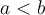 y
y 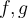 dos funciones integrables, si
dos funciones integrables, si 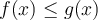 para todo
para todo ![x \in [a,b] x \in [a,b]](https://eva.fing.edu.uy/filter/tex/pix.php/af3c1adca188345d2a91c0d13a891b9f.png) entonces
entonces 
La negación de la afirmación III seria que  para todo
para todo ![x \in [-2,0] x \in [-2,0]](https://eva.fing.edu.uy/filter/tex/pix.php/dc2b8c178b41242eac0995055ee6cdc7.png) por lo que aplicando la propiedad anterior a
por lo que aplicando la propiedad anterior a  constante tendriamos que
constante tendriamos que
lo que es una contradicción.
Concluimos asi que existe ![c \in [-2,0] c \in [-2,0]](https://eva.fing.edu.uy/filter/tex/pix.php/0be57e5958e8d7273984d579b4d3d4af.png) tal que
tal que 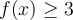
Cualquier cosa vuelve a escribir
Saludos