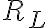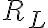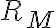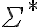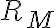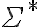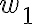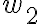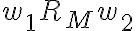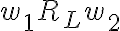Hola,
Tenía una consulta sobre la parte ii. ¿Podemos decir que como no llegan al mismo estado en el autómata entonces no están relacionados por L? O solo puedo decir que si llegan al mismo estado entonces están relacionados por L (como dice la parte A)?
Saludos,
Joel
¡Tranqui! :D
Respuesta corta: si el autómata es mínimo (y completo), basta con que te fijes si ambas tiras terminan en el mismo estado para saber si están relacionadas o no según 
.
Respuesta larga: Bueno, como comentó Diego acá, las clases de 
coinciden con las de 
si el autómata es mínimo (y completo). Eso quiere decir que la partición (en conjuntos) de 
que genera va a coincidir con la que genera 
. Es decir que entonces las tiras de 
que están en cada una de esos conjuntos (las clases) va a coincidir tanto para como para y por lo tanto que las expresiones regulares que generan esos conjuntos también van a coincidir (serán equivalentes, generarán los mismos conjuntos). Ese pique es el que se usa para cuando les pedimos que den las expresiones regulares para las clases de .
Además todo eso quiere decir que una vez que minimizaste el autómata podés usar la definición de sobre ese autómata para evaluar si dos tiras 
y 
están relacionadas (
). Los dos resultados posibles pueden ser:
y terminan de ser procesadas en el mismo estado termina en un estado y en otro
.hola:
para complementar un poco la respuesta (sobre algo que no se preguntó :-D):
aunque el autómata no fuese mínimo, también se podrían extraer conclusiones según el lugar a donde lleguen las tiras al ser procesadas. RM es siempre un refinamiento de RL, con lo que, hablando mal y pronto, si sigma* fuese una torta y RM y RL dos formas de cortarla, cada pedazo que define RL está compuesto por uno o más pedacitos de RM.
esto nos permite decir que, si dos tiras llegan al mismo estado ---pertenecen a la misma clase de RM--- seguramente pertenezcan a la misma clase de RL. ahora, si llegan a estados distintos no podemos decir nada, porque sus respectivas clases RM pueden estar "juntas" en RL. de hecho, es lo que se hace en el algoritmo de minimización: juntar estados "iguales" es lo mismo que decir "ambos son partes de la misma clase de RL".
saludos,
d.-