Parcial 2020 ej 2 V2

Parcial 2020 ej 2 V2

de Martín Ezequiel Rodriguez Raffo -
Número de respuestas: 3

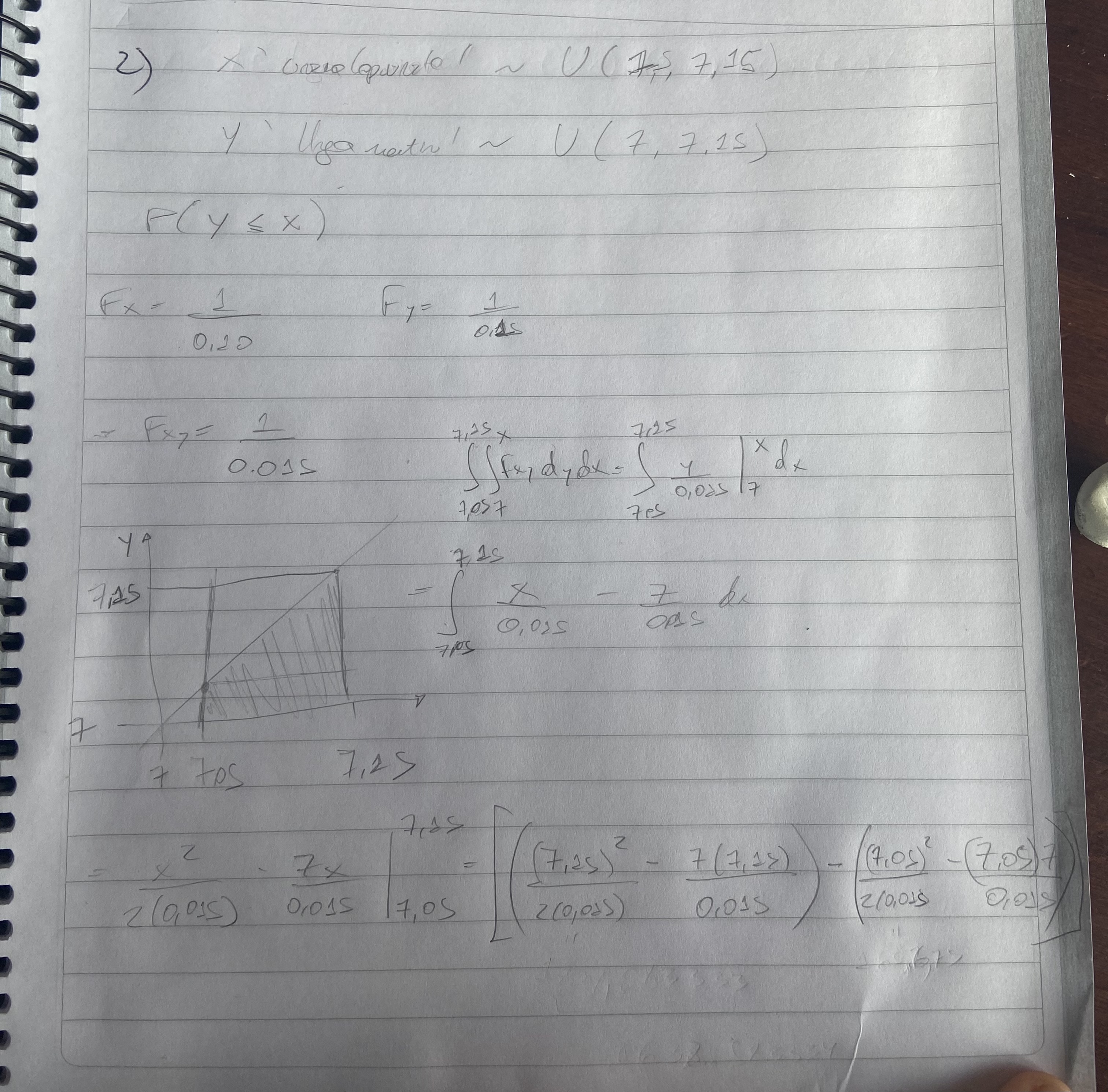
Buenas tardes, estoy intentando hacer este ejercicio pero no me sale. Lo que pensé fue que para que Martin pueda vacunarse debe llegar entre las 7 y 7.15 antes que se cierra la puerta, lo cual pasa entre 7.05 y 7.15.

Llame X a que se cierra la puerta que es una va uniforme de (7.05-7.15) e Y la hora de llegada de Martin que es una va uniforme de (7-7.15) entonces halle la probabilidad que Y sea menor igual que X, integrando fxy en el área que rayé. Las cuentas no me dan el resultado, que podría estar haciendo mal?


Gracias, Martin. 





En respuesta a Martín Ezequiel Rodriguez Raffo

Re: Parcial 2020 ej 2 V2

de Juan Kalemkerian -

Hola Martín.

Ambas variables que definís (X e Y) son uniformes entre 7 y 715.

Ojo que 7,15 no quiere decir las 7 horas y 15 minutos (en todo caso sería 7,25).

Te conviene definr (te simplifica, igual lo podés hacer de la otra forma) X= cantidad de minutos pasadas las 7 en las que llega el vacunador, sería U(0,0.15) e Y= cantidad de minutos pasadas las 7 en las que llega Martín (también U(0,0.15)).

Para que Martín pueda vacunarse hoy o bien debe ocurrir que $$\{Y<5,X<5 \}$$ (es decir que el vacunador llega antes de las 7:05 y Martín también llega antes de las 7:05) o bien debe ocurrir que $$\{X>5, Y<X\}$$ (el vacunador llega después de las 7:05 y Martín llega antes que el vacunador).

$$P(Y<5,X<5 )=P(X<5)P(Y<5)$$ porque X e Y son independientes.

$$P(X>5, Y<X)$$ hacés el dibujo como en la hoja que nos mostrás y calculás la integral doble ahí.

Fijáte a ver si sale, cualquier cosa la seguimos.

Saludos, Juan.

 
En respuesta a Juan Kalemkerian

Re: Parcial 2020 ej 2 V2

de Andres Martínez Manfro -
No logro ver la integral doble, la primera parte la entendí perfecto pero para la segunda no logro visualizarlo
En respuesta a Andres Martínez Manfro

Re: Parcial 2020 ej 2 V2

de Juan Kalemkerian -

Hola Andrés.

Primero dibujáte el cuadrado $$[0,15]\times [0,15]$$, luego en la integral en la región $$\{X>5, Y<X\}$$.

La integral doble te queda $$\int_5^{15} dx \int_0^x \frac{1}{15^2}dy.$$