Foro de parciales y exámenes anteriores

Hola Santiago, el razonamiento está esencialmente bien.
Como el núcleo tiene dim=1, esto dice que 0 es un val.p. y que mg(0)=1.
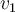Entonces puedes tomar un vec.p. de T asociado al val. p. 0 ( )y agregar otro vector del espacio 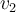para completar una base.
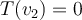Lo que no puede ser es que  también , sino ambos vectores estarían en el núcleo y no formarían una base (que es lo que sugiere tu escritura, que esos dos vectores forman una base que llamas $B=\{v_1,v_2\}$).
En ese caso en la matriz que escribes tiene que ser x=0, aunque no afecta lo fundamental, que la traza vale 0.
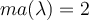Un razonamiento mas compacto es juntar que (nos dice que hay un único val.p.) y que 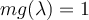, (nos dice que 0 es val.p.).

Espero haber sido de ayuda.

Saludos

J.