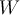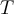Entonces todo el plano xy es un subespacio invariante bajo  , dado que cualquier vector del plano al ser rotado sigue en el plano.
, dado que cualquier vector del plano al ser rotado sigue en el plano.
 , dado que cualquier vector del plano al ser rotado sigue en el plano.
, dado que cualquier vector del plano al ser rotado sigue en el plano. Hay algún vector en el plano que al rotarlo un ángulo 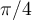 quede en la misma dirección que tenia antes (sino no podría ser
quede en la misma dirección que tenia antes (sino no podría ser 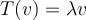 )?
)?
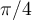 quede en la misma dirección que tenia antes (sino no podría ser
quede en la misma dirección que tenia antes (sino no podría ser 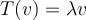 )?
)?Si piensas en este ejemplo tendrás la respuesta que buscas.
Saludos
J.