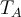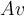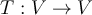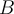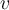GAL2-1S: VEPs de una TL y su matriz asociada.

Buen dia, que tal?

El semestre anterior curse GAL 2 y tengo anotado que en el teorico de Florencia se hizo la siguiente observacion:

Ahora me encuentro haciendo un parcial y resulta que se niega esto, dejo la letras del parcial:

En particular me estoy refiriendo a la afirmación 2 que, según las respuestas del propio parcial es falsa, podrian explicarme mejor por qué? Dado que la respuesta del PDF con las respuestas es bastante breve.

Un saludo, gracias.

Re: VEPs de una TL y su matriz asociada.

de Juan Piccini - martes, 18 de abril de 2023, 10:42

Hola Luca, esos apuntes están bien (salvo un pequeño detalle), creo que los interpretas mal.
El detalle: en el primer renglón debe decir

v≠Ov≠O.
Fuera de eso, los apuntes refieren a la TL

$T_A:\mathbb{K}^n\rightarrow\mathbb{K}^n: T_A(v)=Av$ .

$T_A$ es la TL que toma un vector de

$\mathbb{K}^n$ y devuelve el vector

$Av$ .

En este caso, la matriz

$A$ no es otra cosa que la matriz asociada a

$T_A$ en base canónica.

Tanto el vector como sus coordenadas viven en el mismo espacio,

$\mathbb{K}^n$ , y si agregamos que la base es la canónica, entonces el vector coincide con sus coordenadas.

Si la base no fuese la canónica, el vector y sus coordenadas serían distintas, aunque ambos viviesen en

$\mathbb{K}^n$

En el parcial que mencionas, tenemos

$T:V\rightarrow V$ y la matriz

$A$ es la matriz asociada a

$T$ en una cierta base

$B$ .

Los vectores propios de

$T$ son polinomios, los vectores propios de

$A$ son vectores en

$\mathbb{R}^3$ .

En dicho caso, lo que sucede con los vec.p. es que

$v$ es vec.p. de

$T$ sii

$coord_B(v)$ es vec.p. de

$A$ , porque una cosa es el vector y otra son sus coordenadas en una cierta base.

Espero haber ayudado a aclarar la confusión.

Saludos