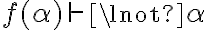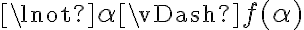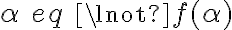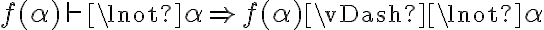Para la parte iii.:
Ahora, tomando las partes (*) y ii. como hipótesis, si se supone por absurdo que 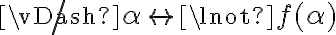 , se puede demostrar con un árbol semántico que se llega a una contradicción. La pregunta es: ¿Es válido usar el árbol semántico? Pregunto porque en la solución hay una demostración bastante más sofisticada, y no me queda claro por qué se haría eso pudiendo usar un árbol.
, se puede demostrar con un árbol semántico que se llega a una contradicción. La pregunta es: ¿Es válido usar el árbol semántico? Pregunto porque en la solución hay una demostración bastante más sofisticada, y no me queda claro por qué se haría eso pudiendo usar un árbol.
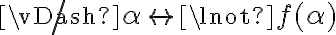 , se puede demostrar con un árbol semántico que se llega a una contradicción. La pregunta es: ¿Es válido usar el árbol semántico? Pregunto porque en la solución hay una demostración bastante más sofisticada, y no me queda claro por qué se haría eso pudiendo usar un árbol.
, se puede demostrar con un árbol semántico que se llega a una contradicción. La pregunta es: ¿Es válido usar el árbol semántico? Pregunto porque en la solución hay una demostración bastante más sofisticada, y no me queda claro por qué se haría eso pudiendo usar un árbol.